
TABLE OF CONTENT :-
1.1- Reflection of Light
1.2- Spherical Mirror
1.3- Refraction of Light
INTRODUCTION
Light:- It is a type of energy, which gives us the sensation of seeing.
Reflection:- When a ray falls on a surface and returns back into the same medium, this phenomenon is called reflection of light.
An object reflects the light falling on it. This reflected light, when received by our eyes, enables us to see the objects.
There are many common and amazing phenomena related to light:-
1 -Formation of image by a mirror.
2 -Twinkling of stars.
3 -Beautiful colours of rainbow.
4 -Bending of light by a medium, etc.
Light appears to travel in a straight line.
Diffraction of light :- If the opaque object placed in the path of light is very small, then the light shows a tendency to bend at its edges instead of moving in a straight line. This effect is called diffraction of light. To explain this effect, light is considered as a wave.
The “modern quantum theory” of light states that light is neither a wave nor a particle. This new theory established a relationship between the particle-related properties of light and its wave nature.
|| 1.1 || TOPIC NO.1-Reflection of Light ||
The mirror reflects most of the light that falls on it.
Law of Reflection:-
(1)- The angle of incidence is equal to the angle of reflection.
(2)-The incident ray, the normal to the mirror at the point of incidence and the reflected ray all lie in the same plane.
These laws of reflection apply to all types of reflecting surfaces including spherical surfaces.
The features of the image formed by a plane mirror are as follows:-
1- Always virtual and straight.
2- Size equal to the size of the object (object).
3- The image will be formed at the same distance behind the mirror as the object (object) is placed in front of the mirror.
4- The image is lateralized.
Meaning of lateral shift:- Lateral shift means change in direction of an object after its image is formed. Right part of the object appears in the left part and left part appears in the right part of the image.
|| 1.2 || TOPIC NO.2- Spherical Mirror ||
Spherical mirrors:- Mirrors whose reflecting surface is spherical are called spherical mirrors.
The reflecting surface of a spherical mirror may be curved inwards or outwards.
Concave Mirror:- The spherical mirror whose reflecting surface is curved inwards i.e. towards the centre of the sphere is called a concave mirror. For example – the inside surface of a spoon.
Convex Mirror:- The spherical mirror whose reflecting surface is curved outwards is called a convex mirror. For example – the raised surface on the outside of a spoon.
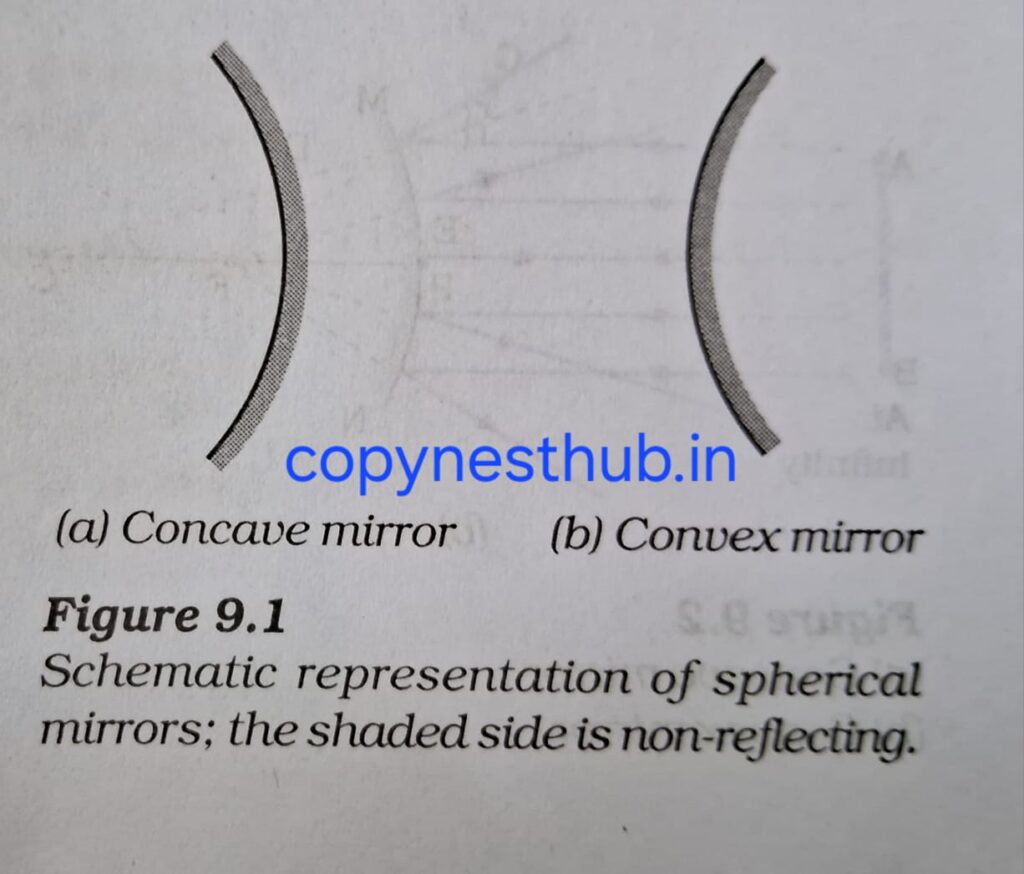
Important terms related to spherical mirrors: –
1- Pole (P)- The center of the reflecting surface of a spherical mirror is called the pole of the mirror. It is located on the surface of the mirror. The pole is usually represented by the letter P.
2- Center of curvature (C)- The reflecting surface of a spherical mirror is a part of a sphere. The center of this sphere is called the center of curvature of the spherical mirror. It is represented by the letter C. The center of curvature is not a part of the mirror. It lies outside the reflecting surface.
The centre of curvature of a concave mirror lies in front of the reflecting surface.
The centre of curvature of a convex mirror lies behind the reflecting surface.
3- Radius of curvature (R)- The radius of the sphere of which the reflecting surface of a spherical mirror is a part is called the radius of curvature of the mirror. It is represented by the letter R.
4- Principal axis- A straight line passing through the pole and radius of curvature of a spherical mirror is called the principal axis of the mirror. The principal axis is the normal to the pole of the mirror.
Principal focus of concave mirror- The light rays coming parallel to the principal axis of the concave mirror meet at a specific point on the principal axis after reflection. This point is called the principal focus of the concave mirror.
Principal focus of a convex mirror- The rays coming parallel to the principal axis of a convex mirror, after reflection, appear to diverge from a point situated on the principal axis. This point is called the principal focus of the convex mirror.
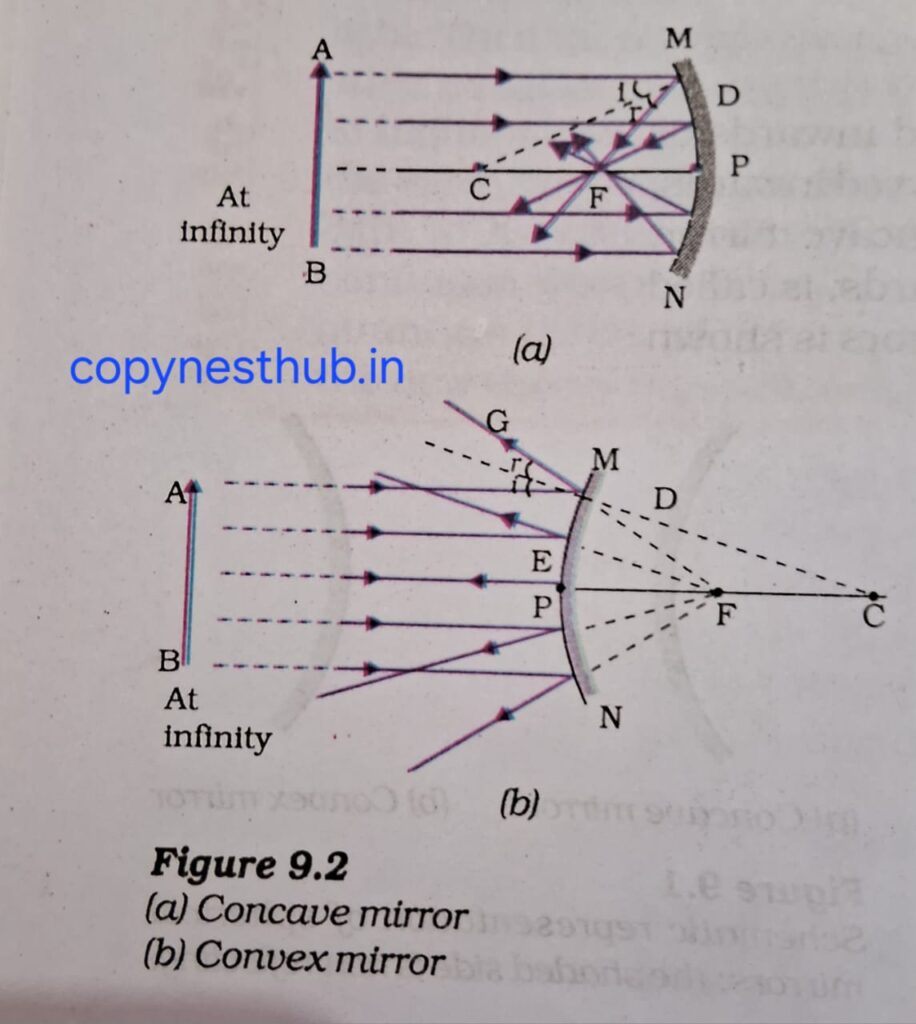
5- Focal length (f)- The distance between the pole and the principal focus of a spherical mirror is called the focal length. It is represented by the letter f.
6. Aperture: The diameter of the circular boundary of the reflecting surface of a spherical mirror is called the aperture of the mirror.
For spherical mirrors of small aperture, radius of curvature (R) is twice the focal length (f). This relation can be expressed as:- (R=2f) This shows that the principal focus of a spherical mirror is the midpoint of the line joining its pole and centre of curvature.
Representation of image formed by a spherical mirror using ray diagrams: –
Every small part of the object acts as a point object. Infinite rays emerge from each of these points. To determine the location of the image of the object, while drawing a ray diagram, some of the large number of rays emerging from a point can be selected as per convenience. For the clarity of the ray diagram, it is more convenient to consider two rays.
The image position of any point object can be found from the intersection of at least two reflecting bodies.
Any two of the following rays may be considered for determining the location of the image :-
1- A ray of light parallel to the principal axis of the mirror after reflection will pass through the principal focus of a concave mirror or will appear to diverge from the principal focus of a convex mirror.

2- The ray passing through the principal focus of a concave mirror or the ray directed towards the principal focus of a convex mirror will emerge parallel to the principal axis after reflection.
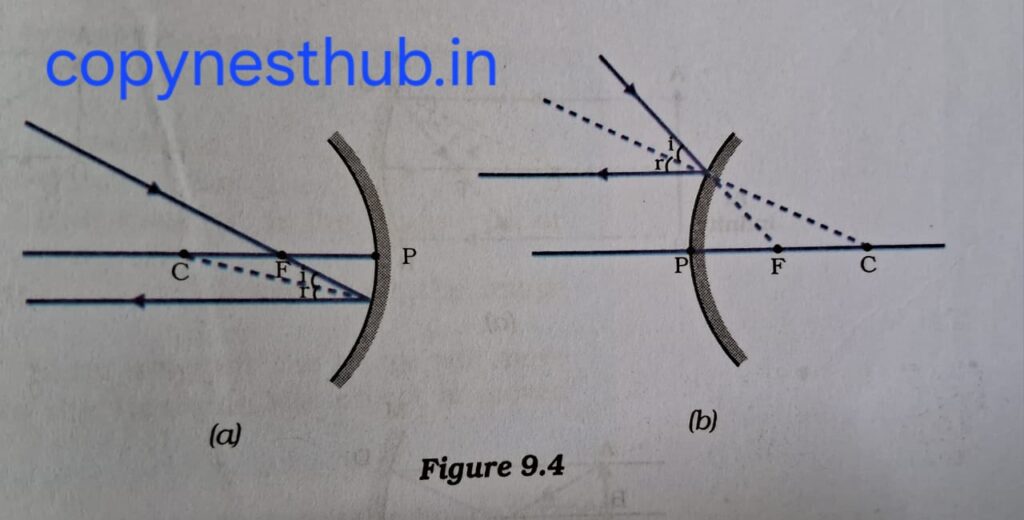
3- A ray passing through the centre of curvature of a concave mirror or a ray directed towards the centre of curvature of a convex mirror, after reflection, is reflected back along the same path.

4- The ray incident in an oblique direction from the principal axis towards the pole of a concave mirror or a convex mirror, gets reflected in the oblique direction only.
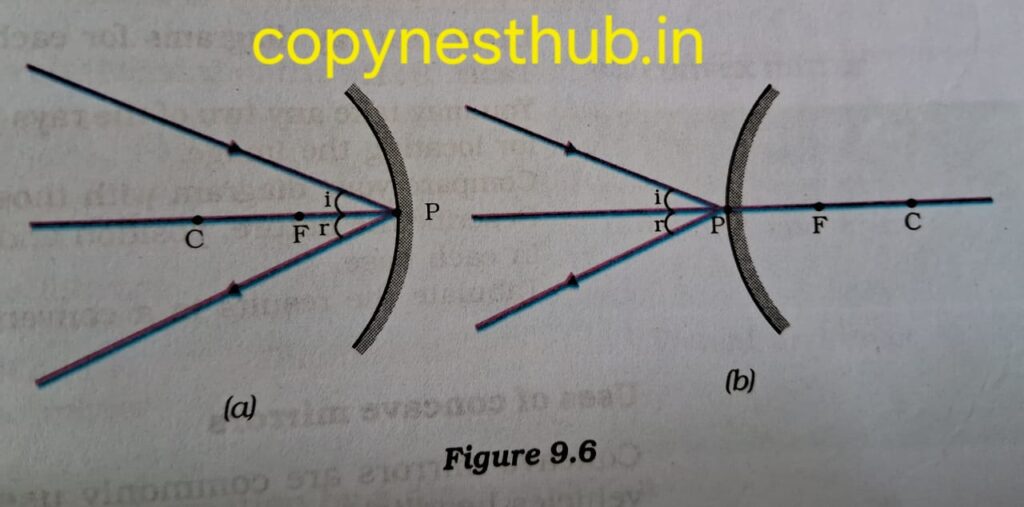
The laws of reflection are followed in all situations.
Images formed by a concave mirror for different positions of the object: –
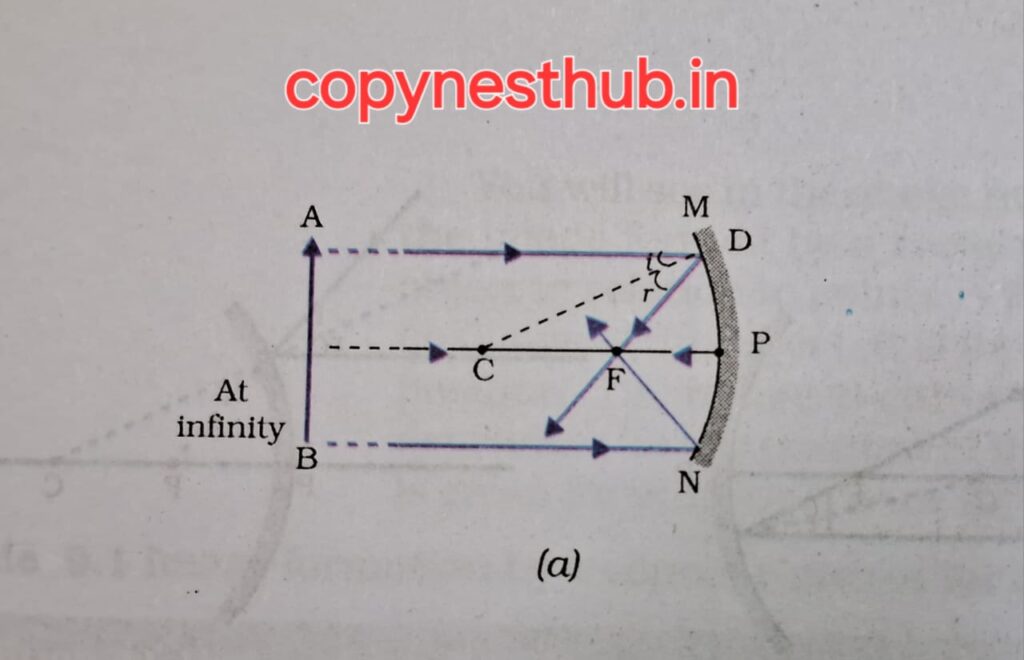
(position of image)- at infinity
(position of image)- at focus F
(size of image)- very small, point size
(nature of image)- real and inverted
(position of image)- beyond C
(position of image)- between F and C
(size of image)- small
(nature of image)- real and inverted
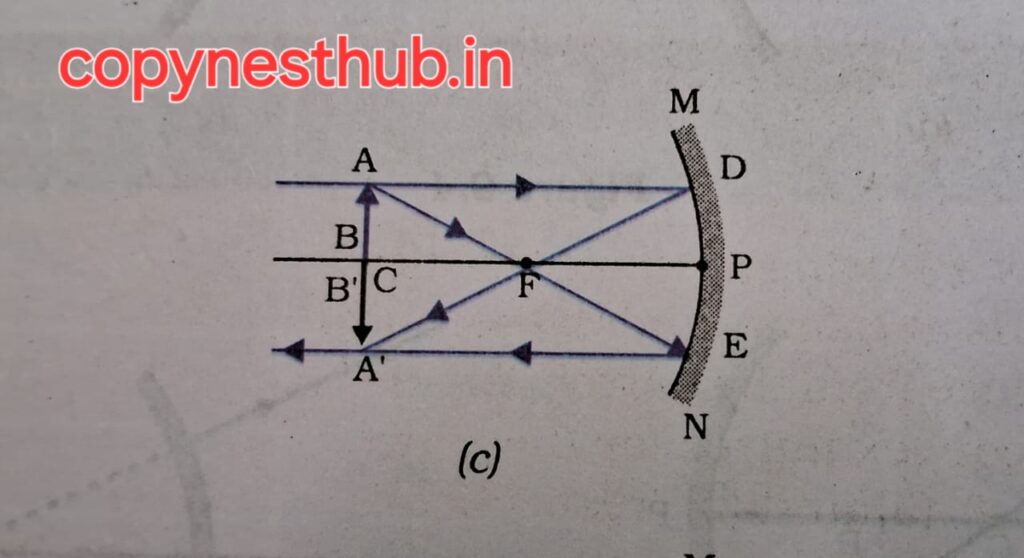
(position of image)- at C
(position of image)- at C
(size of image)- same size
(nature of image)- real and inverted
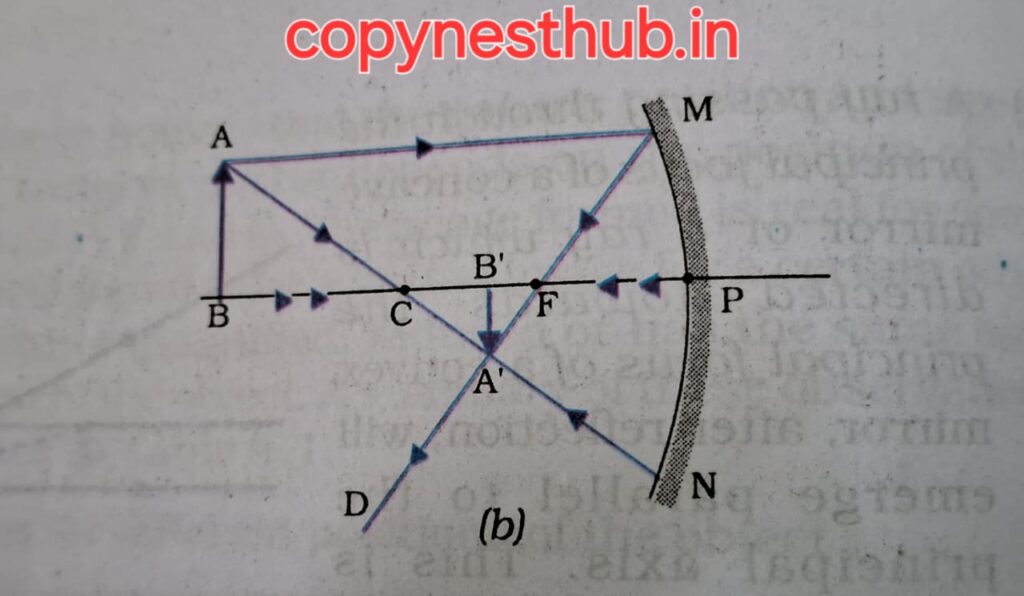
(position of image)- between C and F
(position of image)- beyond C
(size of image)- magnified (large)
(nature of image)- real and inverted
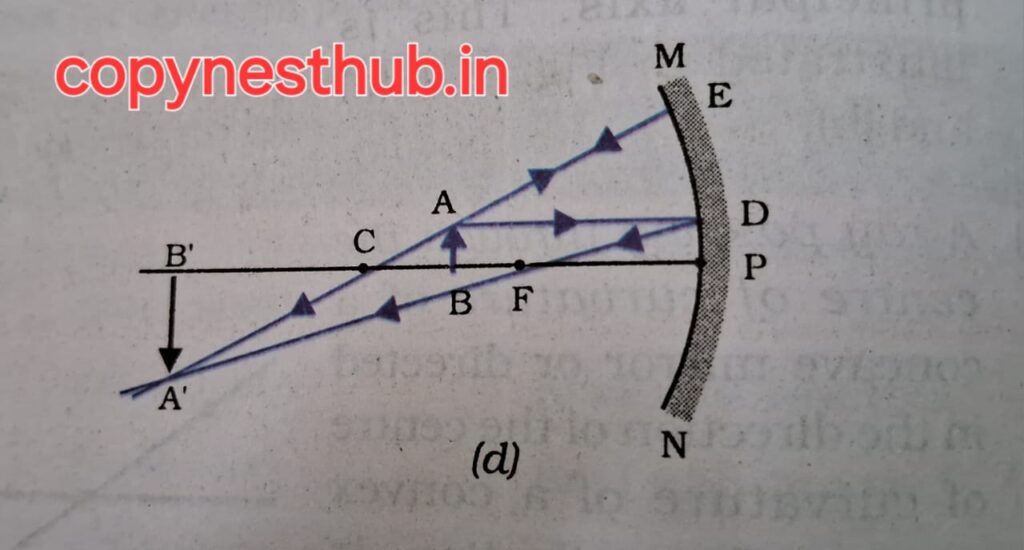
(position of image)- at F
(position of image) at infinity
(size of image)- highly magnified
(nature of image)- real and inverted
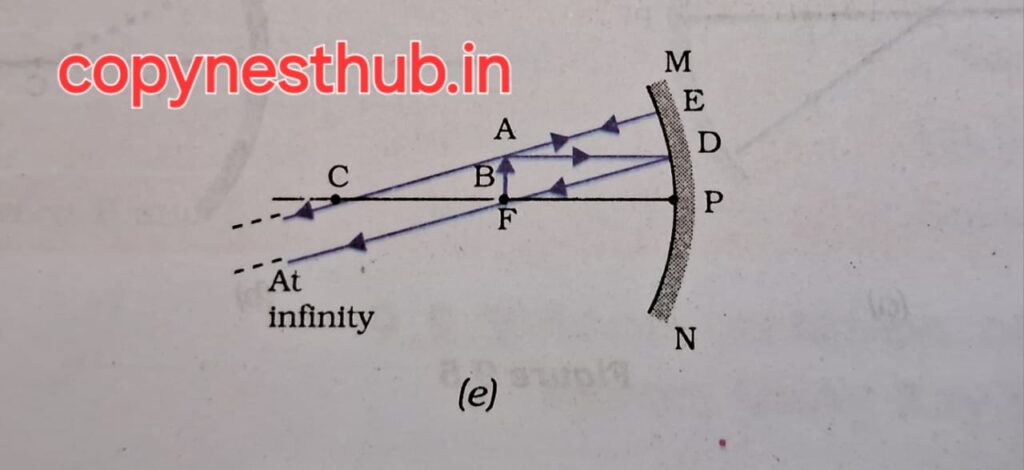
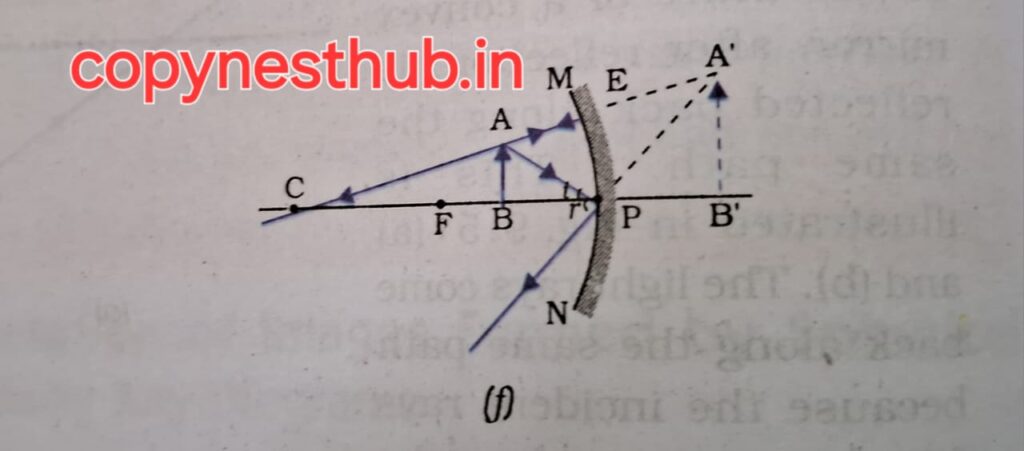
(position of image)- between P and F
(position of image)- behind the mirror
(size of image)- magnified (large)
(nature of image) virtual and erect
Uses of concave mirror:-
1- Torch
2- Search light
3- Vehicle headlight
4- Shaving mirror
5- Solar furnace etc.
Images formed by a convex mirror for different positions of the object: –
(Position of image)- At infinity
(Position of image)- Behind the mirror at focus F
(Size of image)- Very small, point size
(Nature of image)- Virtual and erect

(Position of image)- Between infinity and pole P of the mirror
(Position of image)- Between P and F Behind the mirror
(Size of image)- Small
(Nature of image)- Virtual and erect
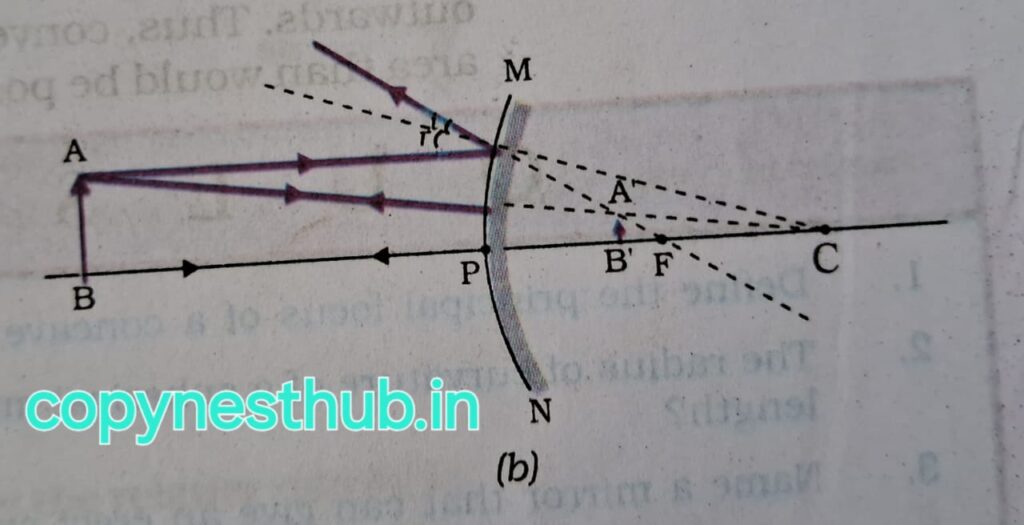
Convex mirrors are used as rear-view mirrors in vehicles.
Convex mirrors are preferred over plane mirrors because they always form a straight image, albeit a small one. Their field of vision is also much larger because they are curved outwards. Thus, convex mirrors enable the driver to see a much larger area behind him as compared to a plane mirror.
Sign convention for reflection by spherical mirrors:-
While considering the reflection of light by a spherical mirror, we will follow a certain sign convention, which is called the new sign convention. In this convention, the pole (P) of the mirror is considered as the origin. The principal axis of the mirror is taken as the x-axis of the coordinate system. This convention is as follows: –
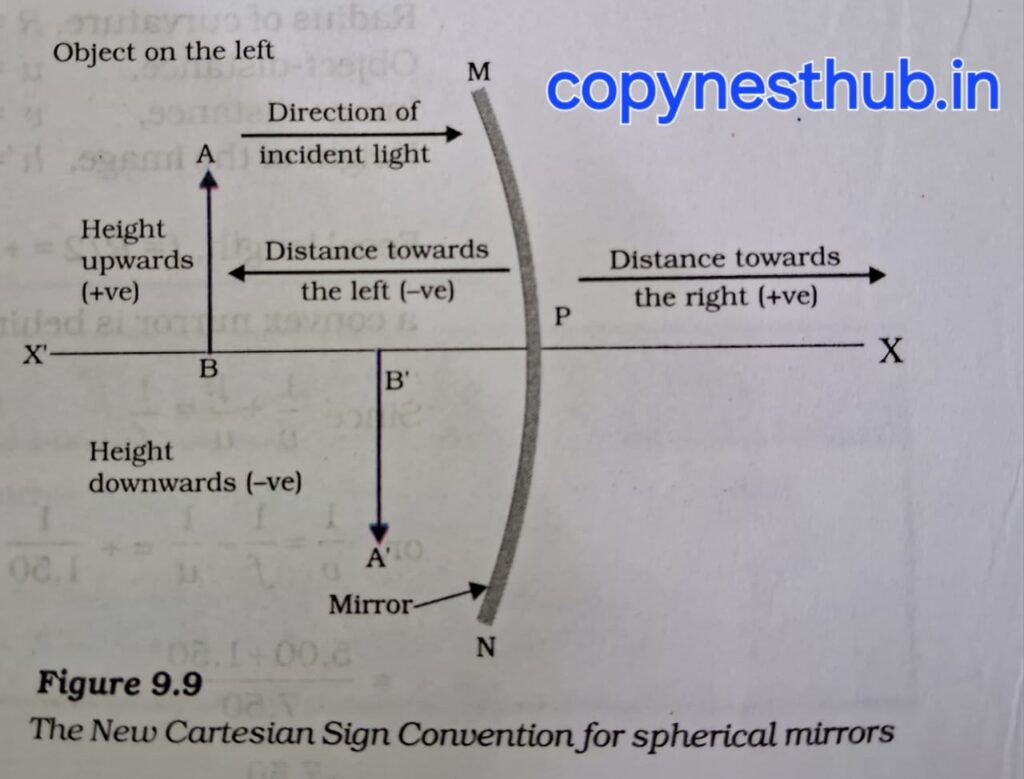
1- The object is always placed on the left side of the mirror. This means that the light from the object on the mirror will be received from the left side.
2- All distances parallel to the principal axis are measured from the pole of the mirror.
3- All distances to the right of the origin are considered positive, while distances measured to the left of the origin are considered negative.
4- Distances measured perpendicular to the principal axis and upwards are considered positive.
5- Distances measured perpendicular to the principal axis and downwards are considered negative.
This sign convention is helpful in deriving the mirror formula and solving the related numerical problem.
Mirror formula and magnification :-
In a spherical mirror, the distance of the object from its pole is called object distance (u).
The distance of the image from the pole of the mirror is called image distance (v).
The distance of the focus from the pole is called the focal length (f).
There is a relationship between these three quantities, which is presented by the mirror formula.
Formula :- 1/v+1/u=1/f
This relation is valid for all types of spherical mirrors and for all positions of the object.
Magnification :-
The magnification produced by a spherical mirror which shows how many times an image is magnified compared to the object.
It is expressed as the ratio of the height of the image and the height of the object.
Formula: Magnification(m)=h’/h
h’= height of the image
h= height of the object
Magnification (m) is also related to object distance (u) and image distance (v). It is expressed as:-
Formula:- m= h’/h= -v/u
For virtual images the height of the object should be taken as positive. For real images the height of the object should be taken as negative.
The negative sign in magnification indicates that the image is real. The positive sign in magnification indicates that the image is virtual.
|| 1.3 || TOPIC NO.3- Refraction of light ||
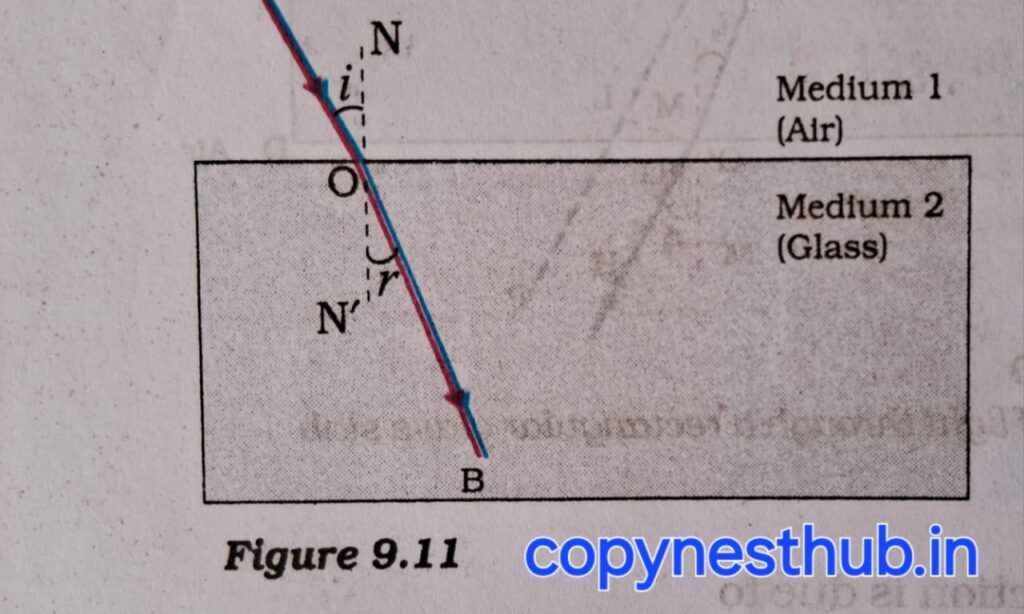
Refraction- When rays of light pass from one medium to another, they deviate from their path, this phenomenon is called refraction of light.

Refraction occurs due to the change in the speed of light when it enters from one transparent medium to another.
Refraction of light occurs on the basis of certain rules. The laws of reflection are as follows: –
1- The incident ray, the reflected ray and the normal at the point of incidence to the surface separating the two media all lie in the same plane.
2- For any fixed colour of light and fixed pair of mediums, the ratio of sine of angle of incidence and sine of angle of refraction is constant. This law is also called “Snell’s law of refraction”. If i is the angle of incidence and r is the angle of refraction, then:-
Sin i/sin r=constant
The value of this constant is called the refractive index of the second medium with respect to the first medium.
Refractive index:-
When a ray of light traveling obliquely enters from one transparent medium to another, it changes its direction in the second medium. The extent of the change in direction for a given pair of media is expressed as the refractive index. It is a constant.
Light travels at different speeds in different mediums. The maximum speed of light in vacuum is 3,00,000km/s. (The fastest speed of light)
The value of refractive index for a pair of two media depends on the speed of light in both the media.
If we consider a ray of light entering from medium 1 to medium 2: –
Suppose the speed of light is v1 in medium 1 and v2 in medium 2. The refractive index of medium 2 with respect to medium 1 is expressed by the ratio of the speed of light in medium 1 and the speed of light in medium 2. It is usually denoted by the symbol n21. It can be expressed in the form of an equation as follows:-
n21=speed of light in medium 1/speed of light in medium 2
n12=speed of light in medium 2/speed of light in medium 1
If medium 1 is a vacuum or air, then the refractive index of medium 2 is considered relative to vacuum. This is called the absolute refractive index of the medium. It is simply denoted by n2. If the speed of light in air is c and the speed of light in the medium is v, then the refractive index of the medium will be nm.
nm=Speed of light in air(c)/Speed of light in medium (v)=c/v
The absolute refractive index of the medium is simply called the refractive index.
1- Refractive index of air 1.003
2- Refractive index of ice 1.31
3- Refractive index of water 1.33
4- Refractive index of alcohol 1.36
5- Refractive index of kerosene 1.44
6- Refractive index of diamond 2.42
The refractive index of water is 1.33 which means that the ratio of the velocity of light in air and the velocity of light in water is 1.33.
The ability of a medium to refract light can also be expressed in terms of its optical density.
When comparing two mediums, the medium with the higher refractive index is optically denser than the other.
The second medium with low refractive index is the light rarer medium. The speed of light in rarer medium is more than that in denser medium, hence the rays of light travelling from rarer medium to denser medium slow down and bend towards the normal. When it travels from denser medium to rarer medium, its speed increases and it moves away from the normal.
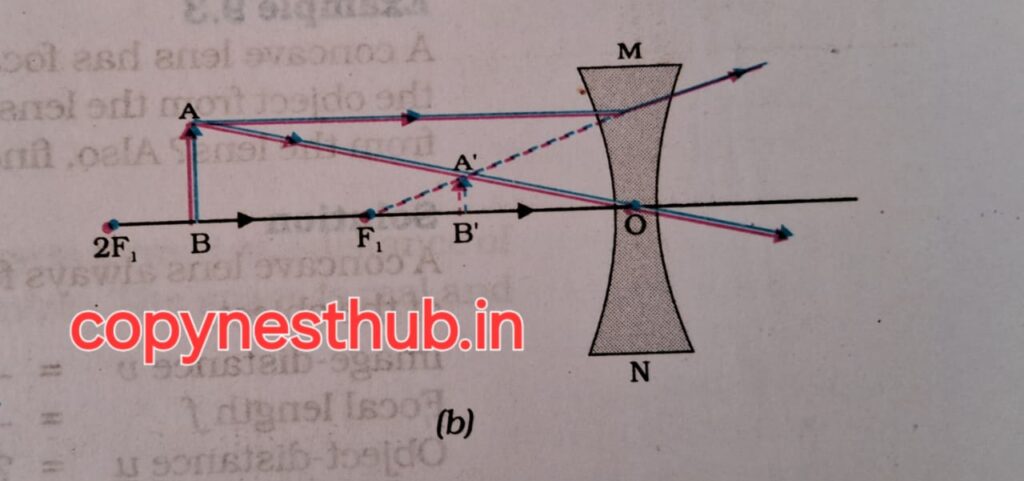
Refraction by a spherical lens:-
Any transparent medium surrounded by two surfaces whose one or both surfaces are spherical is called a lens.
A lens may have two spherical surfaces projecting outwards. Such a lens is called a bi-convex lens. It is also called simply a convex lens. It is thicker in the middle than at the edges. It is also called a converging lens.
A bi-concave lens is surrounded by two spherical surfaces curved inwards. It is also called a concave lens. It is thicker at the edges than in the middle. It is also called a diverging lens.
Any lens, whether convex or concave, has two spherical surfaces. Each of these surfaces is a part of a sphere. The centers of these spheres are called the centers of curvature of the lens.
The centre of curvature of a lens is often denoted by the letter C, since a lens has two centres of curvature they are denoted by C1 and C2.
An imaginary straight line passing through both the centres of curvature of a lens is called the principal axis of the lens.
The central point of the lens is called its optical centre. It is often denoted by the letter O.
The light ray passing through the optical centre of the lens emerges without any deviation.
The effective diameter of the circular outline of a spherical lens is called its diameter.
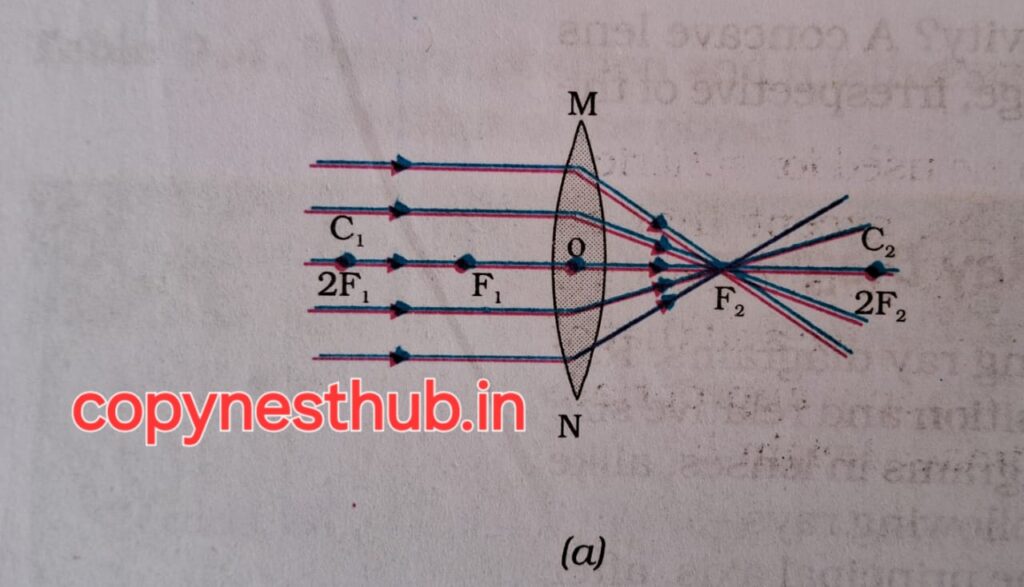
Many rays of light parallel to the principal axis are incident on a convex lens. These rays converge at a point on the principal axis after refraction in the lens. This point on the principal axis is called the principal focus of the lens.
Many rays of light parallel to the principal axis are incident on a concave lens. After refraction from the lens, these rays appear to diverge from a point on the principal axis. This point on the principal axis is called the principal focus of the concave lens.
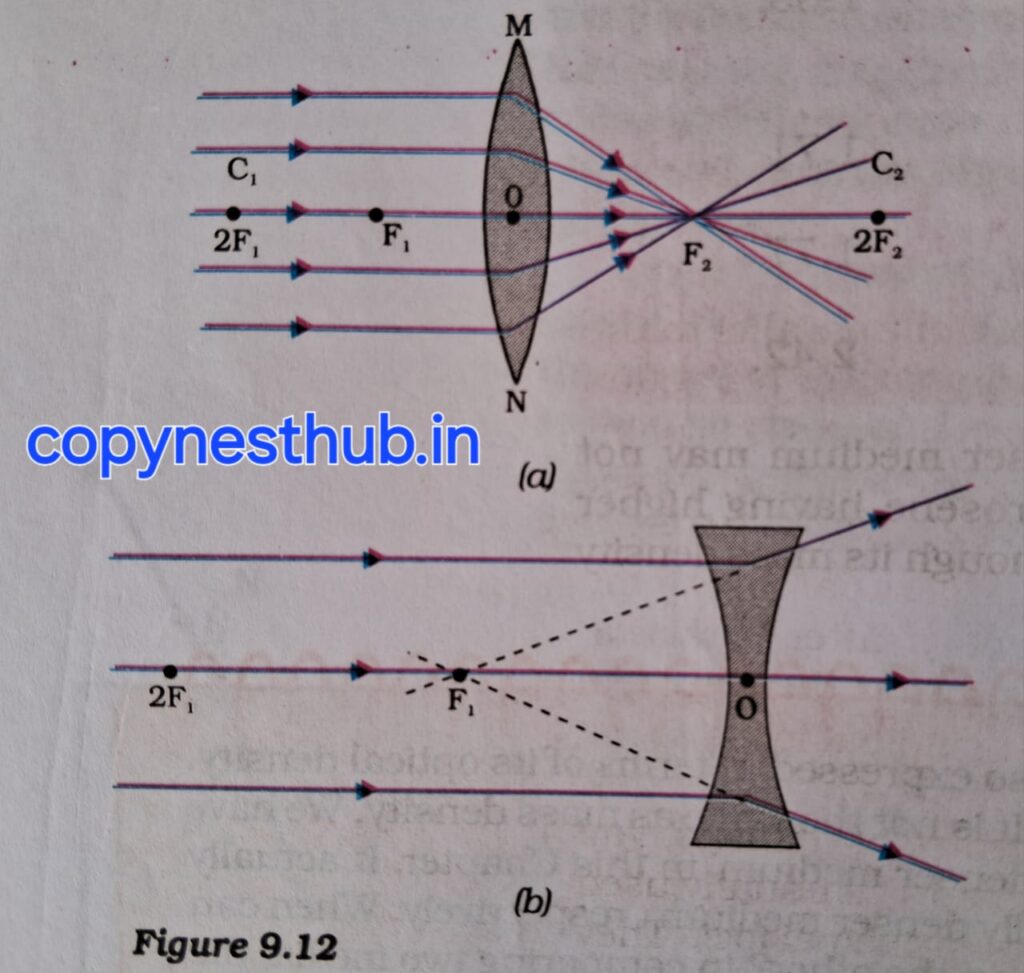
A lens has two principal focuses. These are denoted by F1 and F2. The distance of the principal focus of a lens from the optical centre is called the focal length. The focal length is denoted by the letter f.
Formation of image from a lens using ray diagrams:-
To draw the ray diagram of a lens we may consider any two of the following rays: –
1- Any light ray coming from the object parallel to the principal axis will pass through the principal focus on the other side of the lens after refraction from a convex lens. In the case of a concave lens, the light ray will appear to diverge from the principal focus located on the same side of the lens.
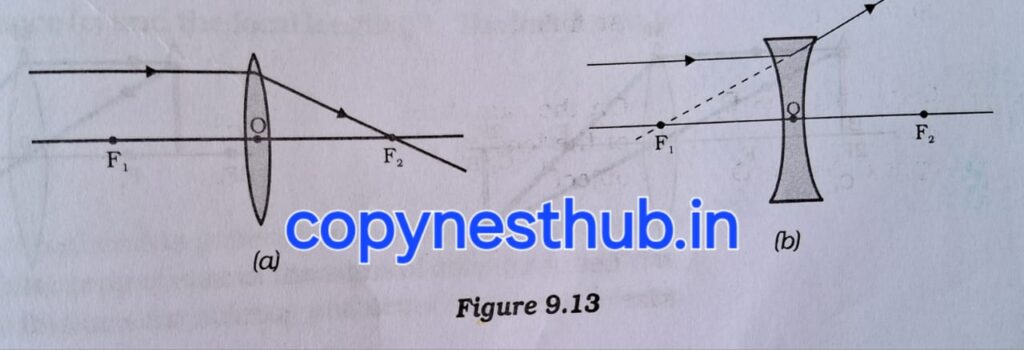
2- The light ray passing through the principal focus will emerge parallel to the principal axis after refraction from the convex lens. The light ray that appears to meet at the principal focus of the concave lens will emerge parallel to the principal axis after refraction.
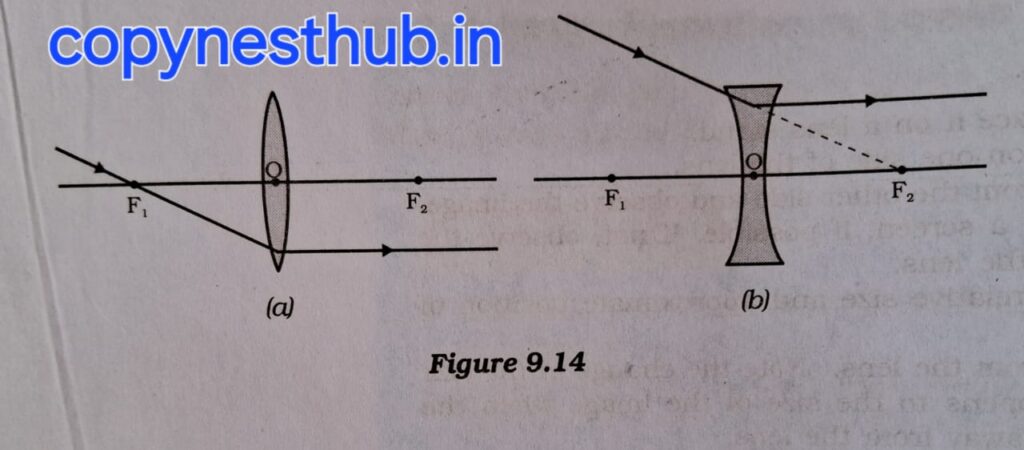
3- The light ray passing through the optical centre of the lens will emerge without any deviation after refraction.
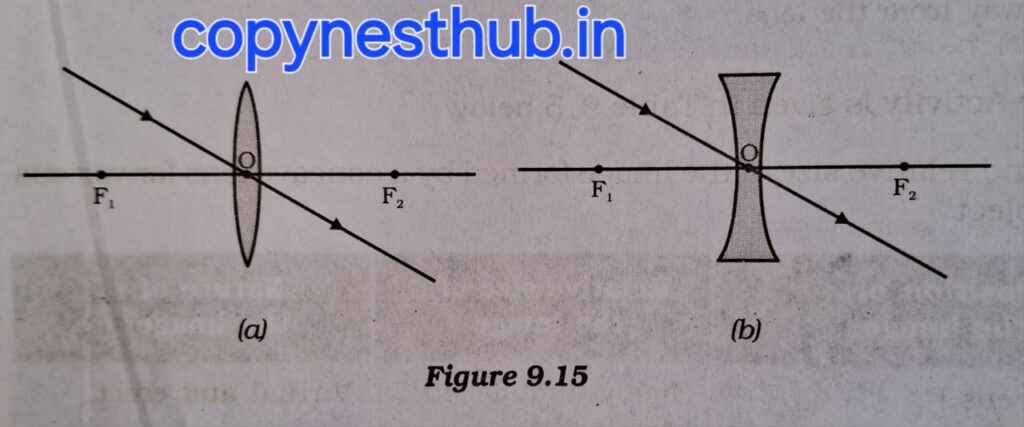
Image formation by lens:-
Lenses form images by refracting light.
The nature, position and expected size of the image formed by a convex lens: –
(position of image) – at infinity
(position of image) Focus F2
(size of image) – very small, point size
(nature of image) – real and inverted
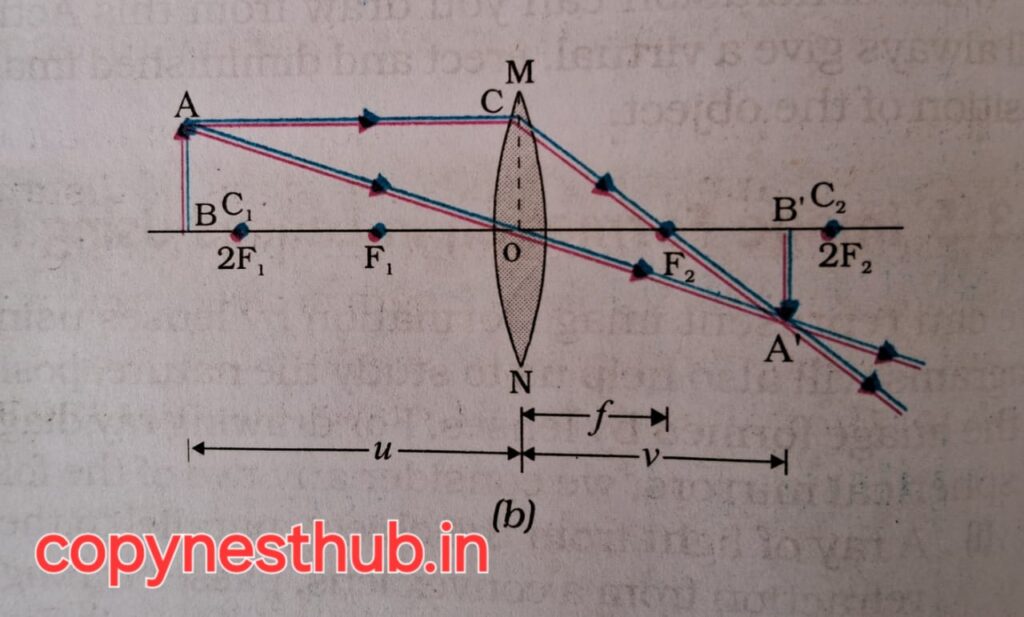
(position of image)- beyond 2F1
(position of image)- between F2 and 2F2
(size of image)- small
(nature of image)- real and inverted
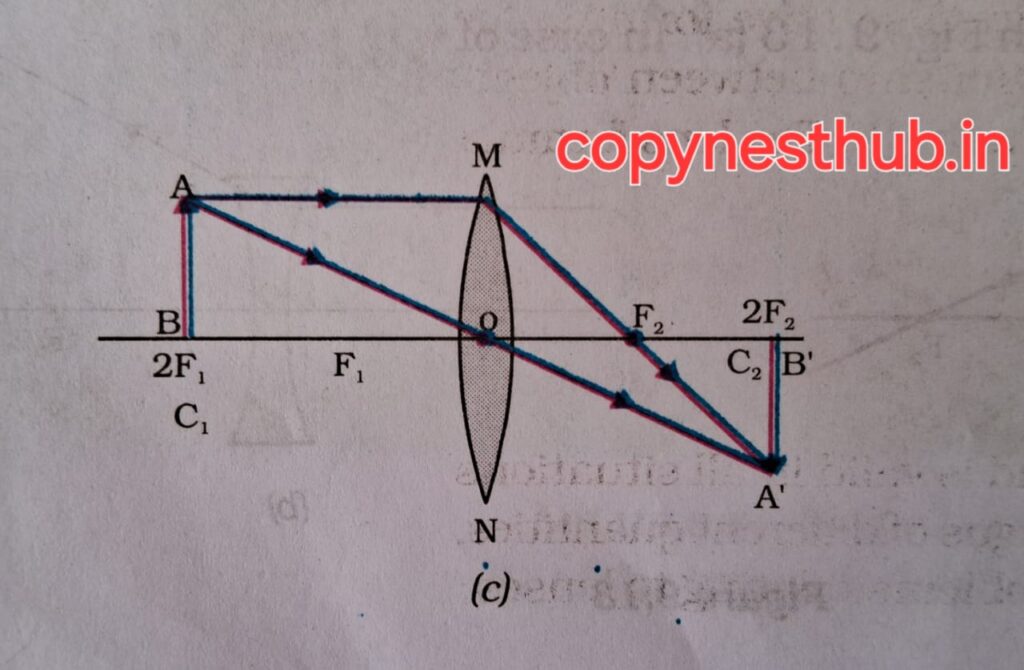
Position of object)- At 2F1
(position of image)- At 2F2
(size of image)- same size
(nature of image)- real and inverted
Position of object)- Between F1 and 2F1
(position of image)- Beyond 2F2
(size of image)- Large (magnified)
(nature of image)- Real and inverted
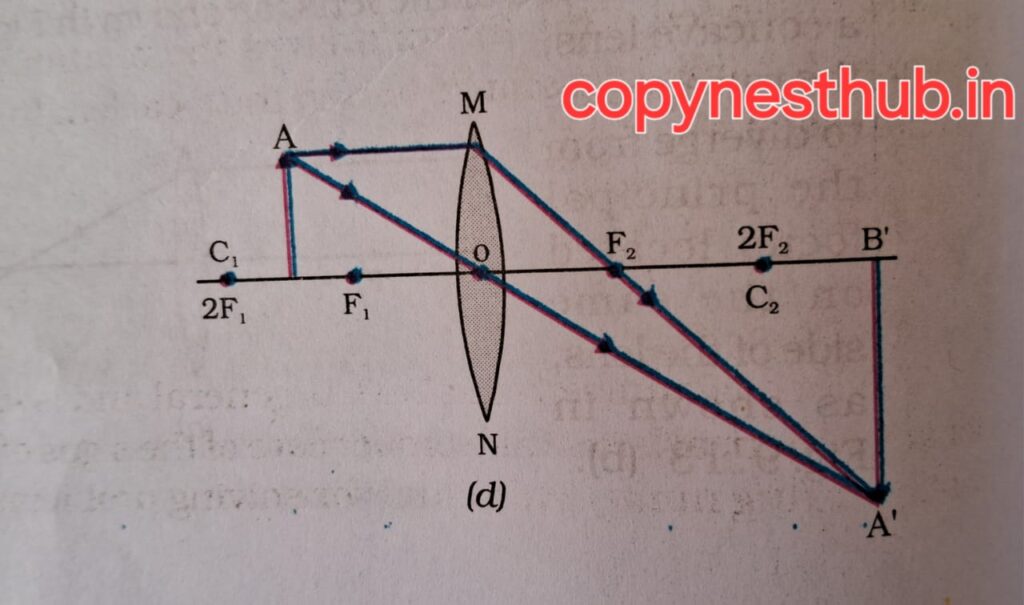
Position of object) – At focus F1
(position of image) – At infinity
(size of image) – Highly magnified
(nature of image) – Real and inverted
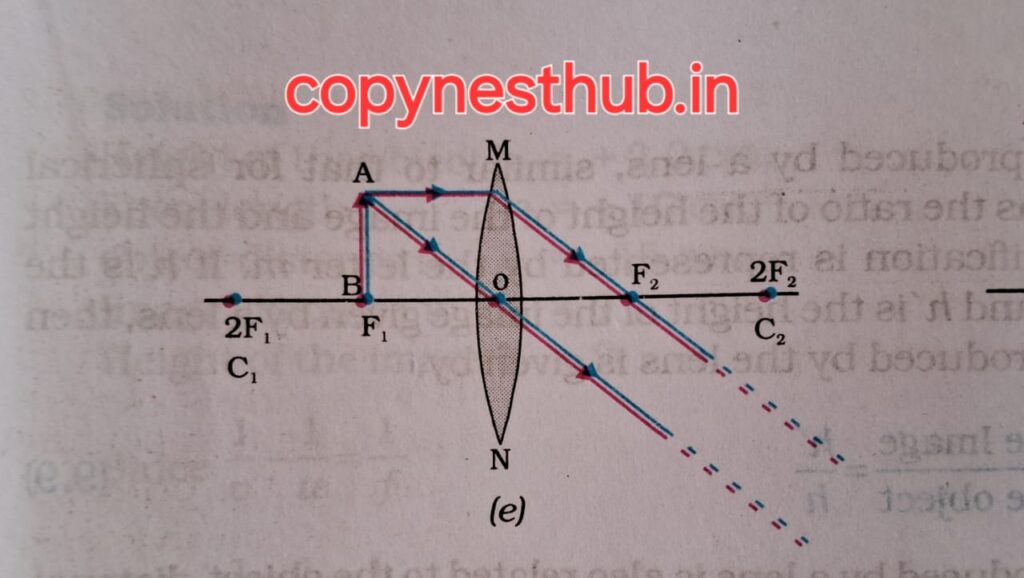
Position of the object- Between focus F1 and optical center O
(Position of the image)- On the same side of the lens as the object
(Size of the image)- Large (magnified)
(Nature of image)- Virtual and erect
The nature, position and expected size of the image formed by a concave lens: –
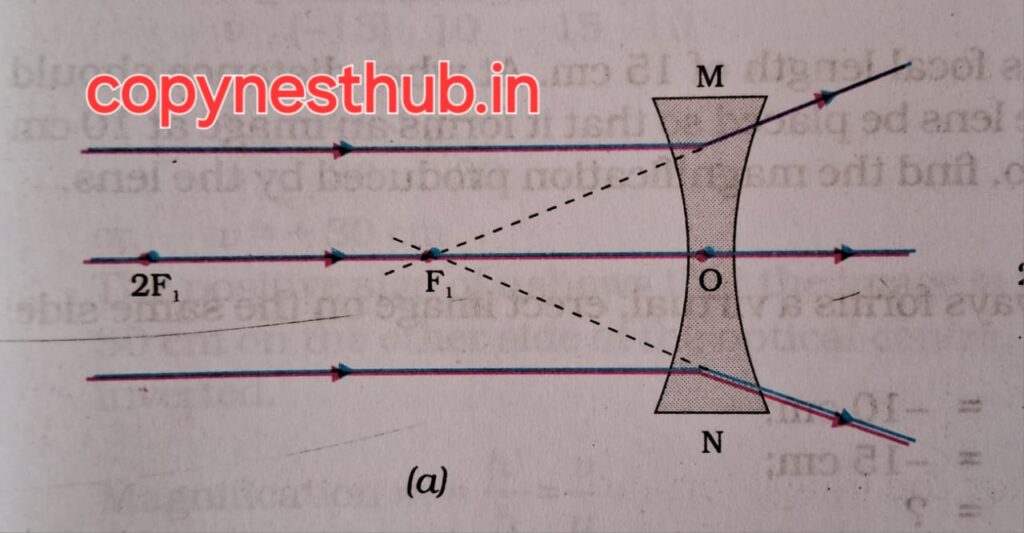
Position of object) – At infinity
(position of image) – At focus F1
(size of image) – Very small, point shape
(nature of image) – virtual and erect
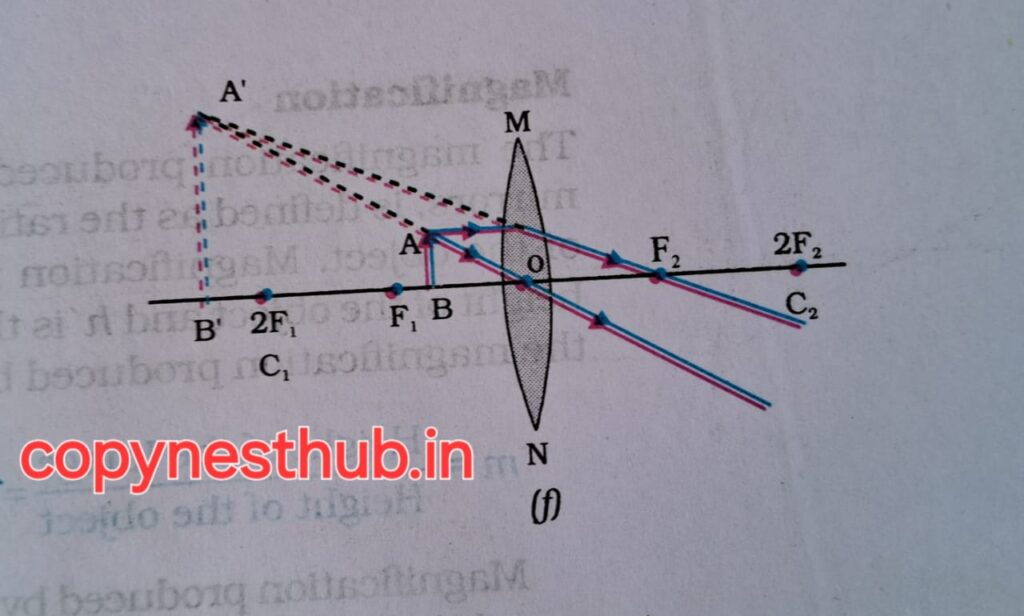
Position of object) Between infinity and optical centre O of the lens
(position of image) Between focus F1 and optical centre O
(size of image) Small
(nature of image) – virtual and erect
Sign convention for spherical lenses:-
Whereas in mirrors all distances are measured from their pole, in lenses all distances are taken from their optical centre.
By convention, the focal length of a convex lens is positive, while the focal length of a concave lens is negative.
Lens formula and magnification:-
There is a relationship between object distance(u), image distance and focal length and these three quantities are represented by the lens formula.
Formula :- 1/v- 1/u=1/f
This lens formula is valid in all situations for any spherical lens.
Magnification :-
If the height of the object is h and the height of the image formed by the lens is h’, then the magnification produced by the lens will be-
Formula :- Magnification (m)=h’/h
Magnification (m) is also related to object distance (u) and image distance (v). It is expressed as:-
Formula:- m= h’/h= v/u
Power of lens :-
The ability of a lens to converge and diverge light rays depends on its focal length.
Example – A convex lens with a short focal length bends light rays through a large angle and focuses them near the optical centre.
The amount to which a lens converges or diverges light rays is expressed as its power. It is represented by the letter P.
The power of a lens of focal length f is:-
Formula:- P=1/f
f is in meters.
The SI unit of lens power is dioptre. It is represented by the letter D.
1 Dioptre is the power of a lens whose focal length is 1 meter.
The power of a convex lens is positive and that of a concave lens is negative.
THANKS FOR READING…