
TABLE OF CONTENT :-
1.1- प्रकाश का परावर्तन
1.2- गोलीय दर्पण
1.3- प्रकाश का अपवर्तन
INTRODUCTION
प्रकाश:- यह एक प्रकार की ऊर्जा है,जो हमें देखने की अनुभूति प्रदान करती है।
परावर्तन:- जब कोई किरण किसी सतह पर आपतित होकर उसी माध्यम में पुनः वापस लौटती है, तो इस परिघटना को प्रकाश का परावर्तन कहते हैं।
कोई वस्तु स्वयं पर पड़ने वाले प्रकाश को परावर्तित कर देती है। यह परावर्तित प्रकाश जब हमारी आंखों द्वारा ग्रहण किया जाता है, तो हमें वस्तुओं को देखने योग्य बनाता है।
प्रकाश से प्रकाश से संबंधित अनेक सामान्य तथा अद्भुत घटनाएं हैं:-
1-दर्पण द्वारा प्रतिबिंब का बनना।
2-तारों का टिमटिमाना ।
3-इंद्रधनुष के सुंदर रंग।
4-किसी माध्यम द्वारा प्रकाश को मोड़ना, आदि।
प्रकाश सरल रेखा में गमन करता प्रतीत होता है।
प्रकाश का विवर्तन:-यदि प्रकाश के पथ में रखी अपारदर्शी वस्तु अत्यंत छोटी हो, तो प्रकाश सरल रेखा में चलने की बजाय उनकी किनारों पर मुड़ने की प्रवृत्ति दर्शाता है।इस प्रभाव को प्रकाश का विवर्तन कहते हैं।इस प्रभाव की व्याख्या करने के लिए प्रकाश को तरंग के रूप में माना जाता है।
प्रकाश का “आधुनिक क्वांटम सिद्धांत” बताता है कि प्रकाश न तो तरंग है और नहीं कण। इस नए सिद्धांत में प्रकाश के कण संबंधित गुण तथा तरंग प्रकृति के बीच संबंध स्थापित किया।
|| 1.1 || TOPIC NO.1-प्रकाश का परावर्तन ||
दर्पण अपने ऊपर पड़ने वाले अधिकांश प्रकाश को परावर्तित कर देता है।
परावर्तन का नियम:-
(1)-आपतन कोण परावर्तन कोण के बराबर होता है।
(2)-आपतित किरण,दर्पण के आपतन बिंदु पर अभिलंब तथा परावर्तित किरण सभी एक ही तल में होते हैं।
परावर्तन के यह नियम गोलीय पृष्ठों सहित सभी प्रकार के परावर्तक पृष्ठों के लिए लागू होते हैं।
समतल दर्पण द्वारा बने प्रतिबिंब की विशेषता निम्न है:-
1-सदैव आभासी तथा सीधा।
2-साइज वस्तु (बिंब) के साइज के बराबर।
3-प्रतिबिंब दर्पण के पीछे उतनी ही दूरी पर बनेगा जितनी दूरी पर दर्पण के सामने वस्तु (बिंब) रखा होता है।
4-प्रतिबिंब पार्श्व परिवर्तित होता है।
पार्श्व परिवर्तित का अर्थ:-पार्श्व परिवर्तन का मतलब है, किसी वस्तु का प्रतिबिंब बनने के बाद उसकी दिशा में बदलाव होना।वस्तु का दायां हिस्सा प्रतिबिंब में बाएं हिस्से में और बायां हिस्सा दाएं हिस्से में दिखाई देना।
|| 1.2 || TOPIC NO.2- गोलीय दर्पण ||
गोलीय दर्पण:- ऐसे दर्पण जिनका परावर्तक पृष्ठ गोलीय है,गोलीय दर्पण कहलाते हैं।
गोलीय दर्पण का परावर्तक पृष्ठ अंदर की ओर या बाहर की ओर वक्रित हो सकता है।
अवतल दर्पण:- वह गोलीय दर्पण जिसका परावर्तक पृष्ठ अंदर की ओर अर्थात गोले की केंद्र की ओर वक्रित है, वह अवतल दर्पण कहलाता है।जैसे – चम्मच के अंदर का पृष्ठ।
उत्तल दर्पण:- वह गोलीय दर्पण जिसका परावर्तक पृष्ठ बाहर की ओर वक्रित है, उत्तल दर्पण कहलाता है।जैसे- चम्मच के बाहर की ओर उभरा पृष्ठ।
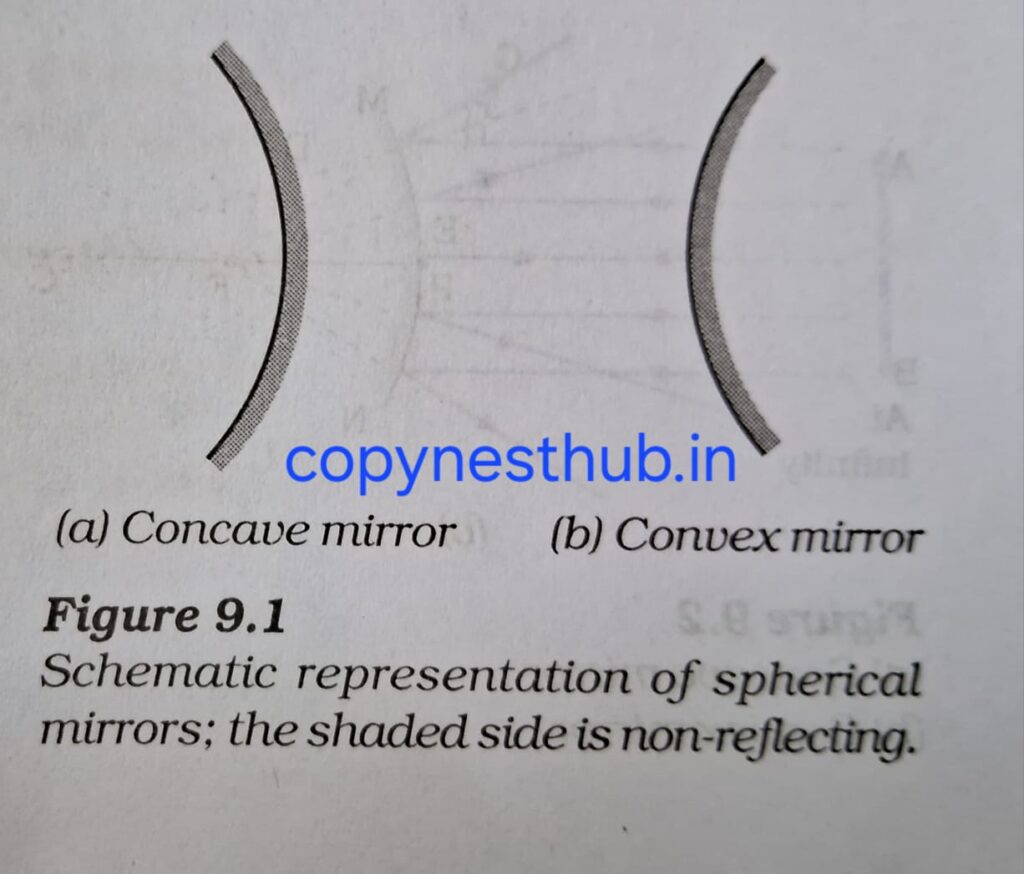
गोलीय दर्पण के से संबंधित महत्वपूर्ण पद: –
1-ध्रुव(P)- गोलीय दर्पण के परावर्तक पृष्ठ के केंद्र को दर्पण का ध्रुव कहते हैं। यह दर्पण के पृष्ठ पर स्थित होता है। ध्रुव को प्राय: P अक्षर से निरूपित करते हैं।
2-वक्रता केंद्र(C)- गोलीय दर्पण का परावर्तक पृष्ठ एक गोले का भाग है। इस गोले का केंद्र गोलीय दर्पण का वक्रता केंद्र कहलाता है। यह अक्षर C से निरूपित किया जाता है। वक्रता केंद्र दर्पण का भाग नहीं होता है। यह परावर्तक पृष्ठ के बाहर स्थित है।
अवतल दर्पण का वक्रता केंद्र परावर्तक पृष्ठ के सामने स्थित होता है।
उत्तल दर्पण का वक्रता केंद्र परावर्तक पृष्ठ के पीछे स्थित होता है।
3-वक्रता त्रिज्या(R)- गोलीय दर्पण का परावर्तक पृष्ठ जिस गोले का भाग है,उसकी त्रिज्या दर्पण की वक्रता त्रिज्या कहलाती है। इसे अक्षर R से निरूपित किया जाता है।
4-मुख्य अक्ष- गोलीय दर्पण के ध्रुव तथा वक्रता त्रिज्या से गुजरने वाली एक सीधी रेखा दर्पण का मुख्य अक्ष कहलाती है। मुख्य अक्ष दर्पण के ध्रुव पर अभिलंब है।
अवतल दर्पण का मुख्य फोकस- अवतल दर्पण के मुख्य अक्ष के समानांतर आने वाली प्रकाश किरणें परावर्तन के बाद मुख्य अक्ष पर एक विशिष्ट बिंदु पर मिलती हैं।यह बिंदु अवतल दर्पण का मुख्य फ़ोकस कहलाता है।
उत्तल दर्पण का मुख्य फोकस- उत्तल दर्पण के मुख्य अक्ष के समानांतर आने वाली किरणें, परावर्तन के बाद मुख्य अक्ष पर स्थित एक बिंदु से विचलित होती हुई प्रतीत होती हैं।इस बिंदु को उत्तल दर्पण का मुख्य फ़ोकस कहते हैं।
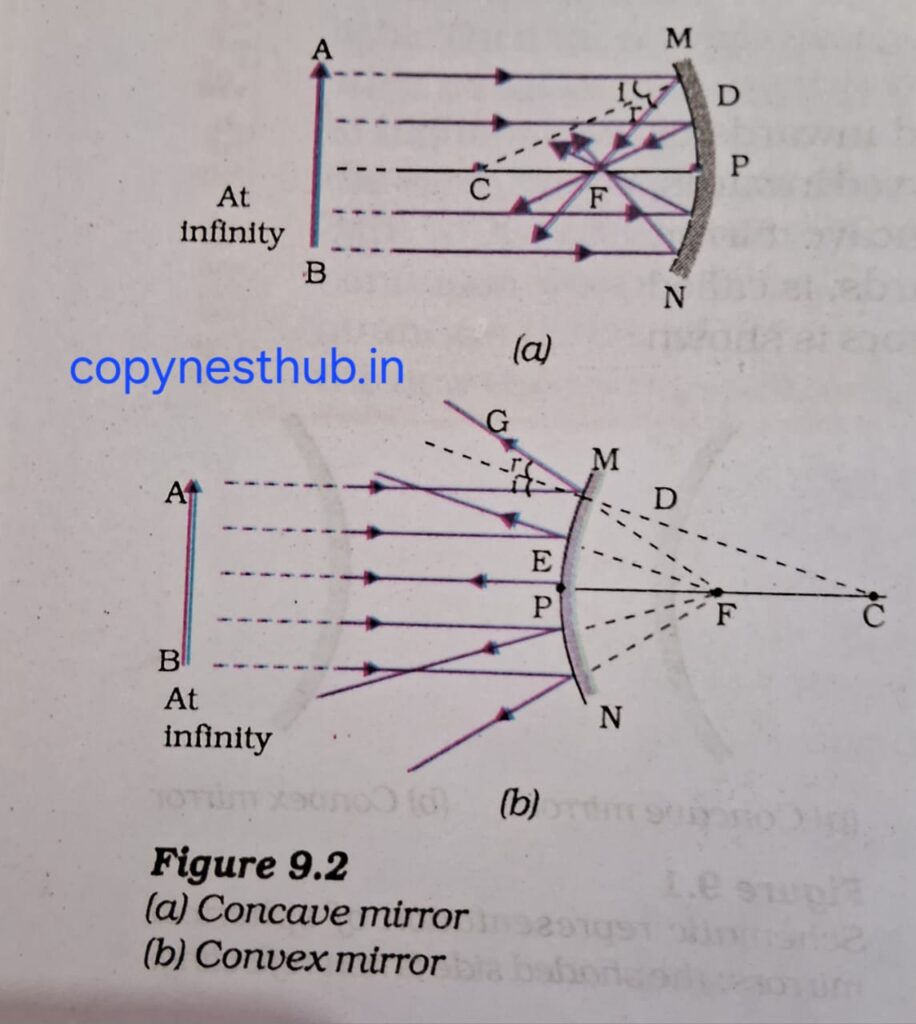
5-फोकस दूरी(f)- गोलीय दर्पण के ध्रुव तथा मुख्य फोकस के बीच की दूरी फोकस दूरी कहलाती है। इसे अक्षर f द्वारा निरूपित किया जाता है।
6-द्वारक – गोलीय दर्पण के परावर्तक पृष्ठ की वृताकार सीमा का व्यास दर्पण का द्वाराक कहलाता है।
छोटे द्वारक के गोलीय दर्पणों के लिए वक्रता त्रिज्या(R) फोकस दूरी(f) से दोगुनी होती है। इस संबंध को व्यक्त किया जा सकता है:- (R=2f ) यह दर्शाता है कि किसी गोलीय दर्पण का मुख्य फोकस उसके ध्रुव तथा वक्रता केंद्र को मिलाने वाली रेखा का मध्य बिंदु होता है।
किरण आरेखों का उपयोग करके गोलीय दर्पण द्वारा बने प्रतिबिंब का निरूपण: –
बिंब का प्रत्येक छोटा भाग एक बिंदु बिंब की भांति कार्य करता है। इन बिंदुओं में प्रत्येक से अनंत किरणें उत्पन्न होती हैं।बिंब के प्रतिबिंब का स्थान निर्धारण करने के लिए, किरण आरेख बनाते समय किसी बिंदु से निकलने वाली किरणों की विशाल संख्या में से सुविधानुसार कुछ को चुना जा सकता है। किरण आरेख की स्पष्टता के लिए दो किरणों पर विचार करना अधिक सुविधाजनक है।
कम से कम दो परावर्तित करने के प्रतिच्छेदन से किसी बिंदु बिंब की प्रतिबिंब की स्थिति ज्ञात की जा सकती है।
प्रतिबिंब के स्थान निर्धारण के लिए निम्न में से किन्हीं भी दो किरणों पर विचार किया जा सकता है: –
1-दर्पण के मुख्य अक्ष के समांतर प्रकाश किरण परावर्तन के पश्चात अवतल दर्पण की मुख्य फोकस से गुजरेगी अथवा उत्तल दर्पण के मुख्य फोकस से अपसरित होती प्रतीत होगी।
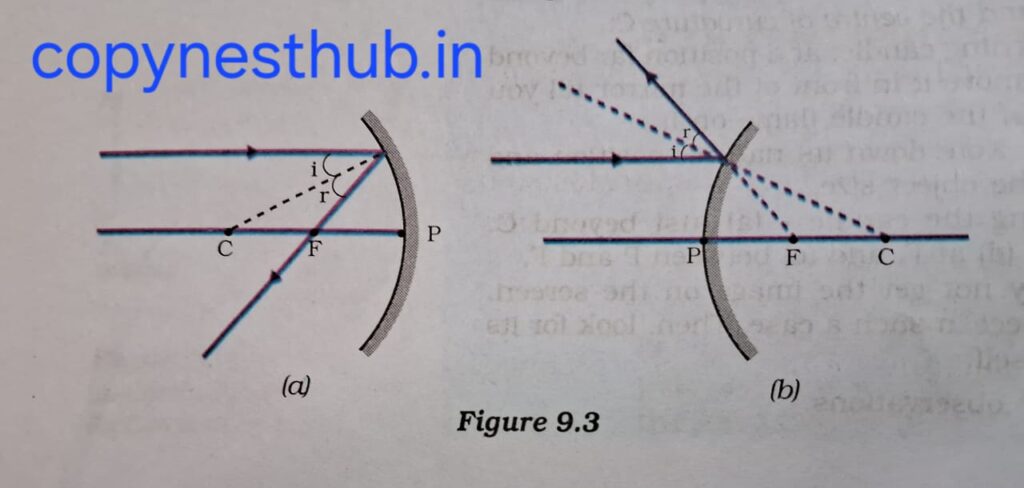
2-अवतल दर्पण के मुख्य फोकस से गुजरने वाली किरण अथवा उत्तल दर्पण के मुख्य फोकस की ओर निर्देशित किरण परावर्तन के पश्चात मुख्य अक्ष के समांतर निकलेगी।
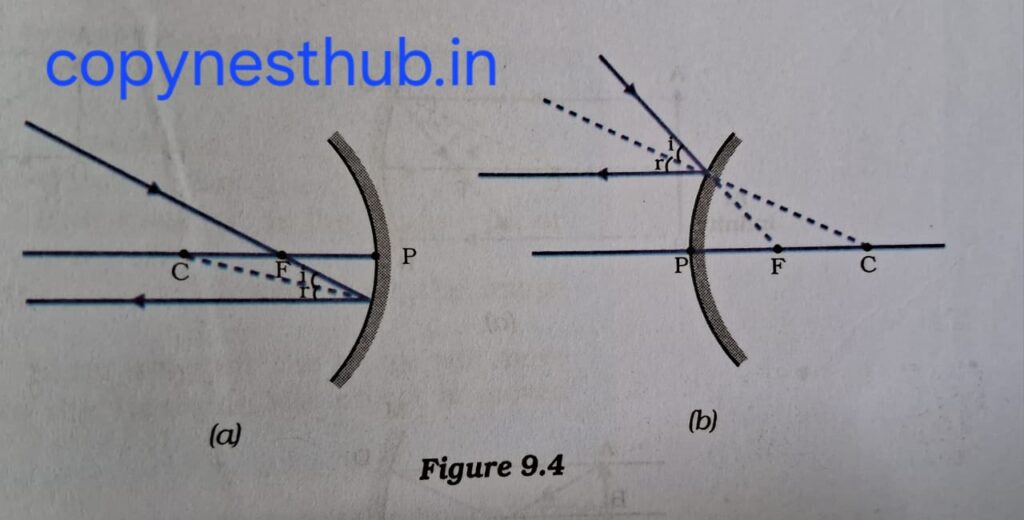
3-अवतल दर्पण के वक्रता केंद्र से गुजरने वाली किरण अथवा उत्तल दर्पण के वक्रता केंद्र की और निर्देशित किरण, परावर्तन के पश्चात उसी पथ के अनुदिश वापस परावर्तित हो जाती है।
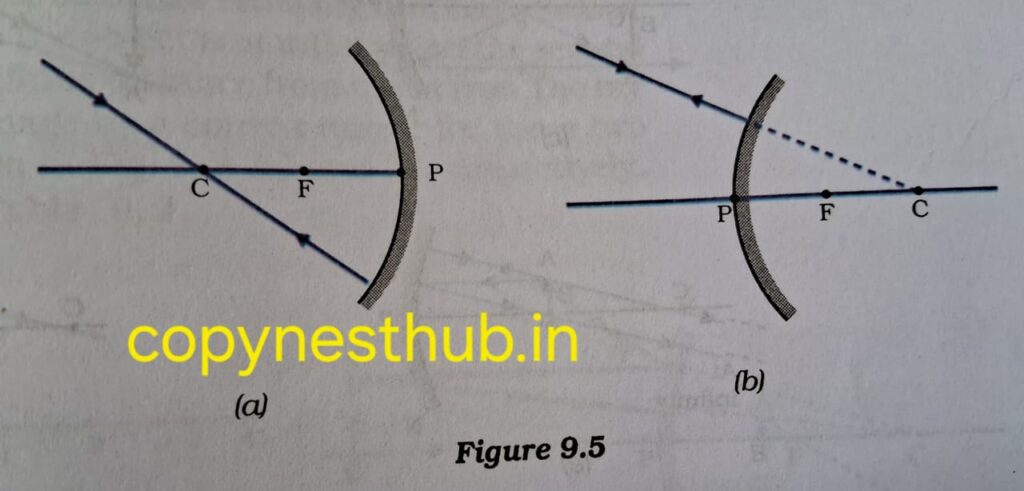
4-अवतल दर्पण अथवा उत्तल दर्पण की ध्रुव की ओर मुख्य अक्ष से तिर्यक दिशा में आपतित किरण, तिर्यक दिशा में ही परिवर्तित होती है।
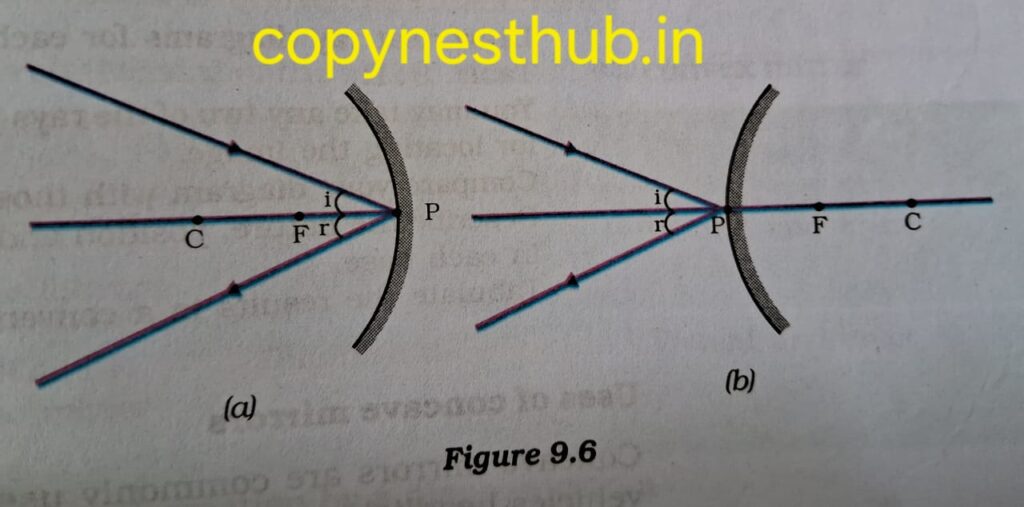
सभी स्थितियों में परावर्तन के नियमों का पालन होता है।
किसी अवतल दर्पण द्वारा बिंब की विभिन्न स्थितियों के लिए बने प्रतिबिंब: –
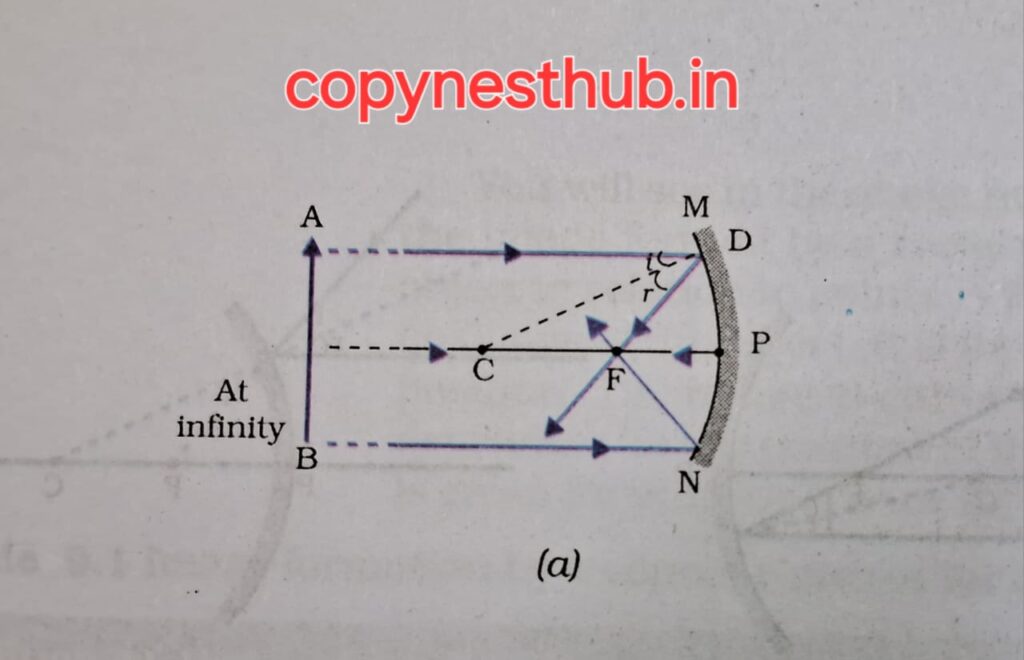
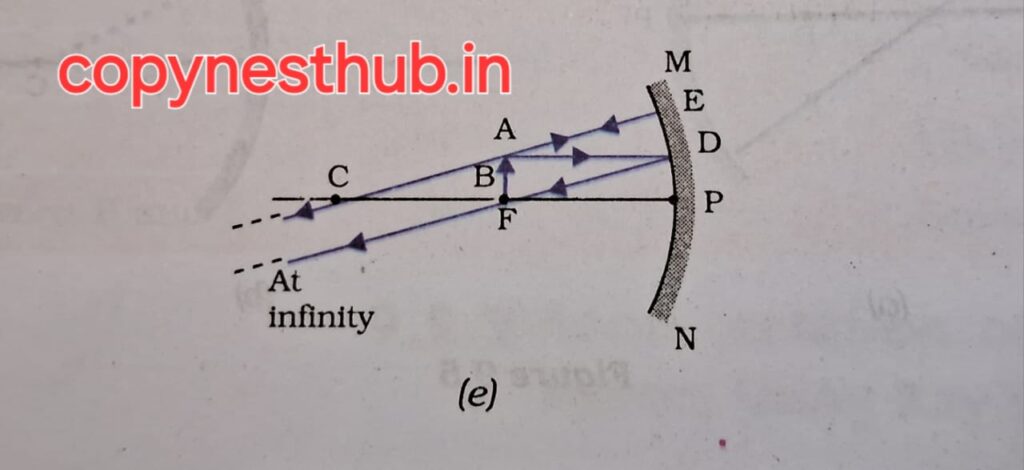
(बिंब की स्थिति)- अनंत पर
(प्रतिबिंब की स्थिति)- फोकस F पर
(प्रतिबिंब का साइज़)- अत्यधिक छोटा,बिंदु साइज
(प्रतिबिंब की प्रकृति)- वास्तविक एवं उल्टा
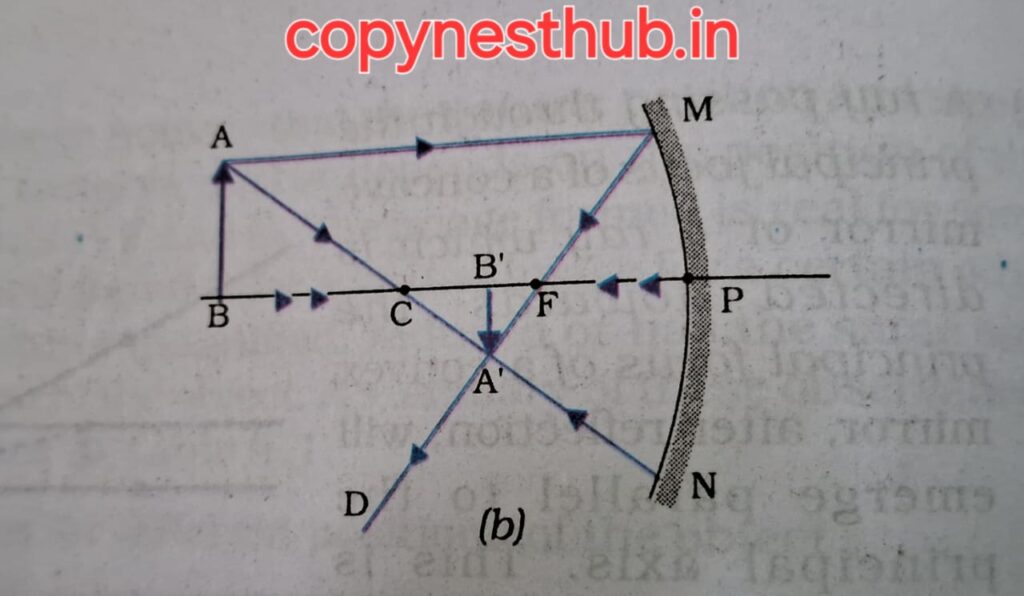
(बिंब की स्थिति)- C से परे
(प्रतिबिंब की स्थिति)- F और C के बीच
(प्रतिबिंब का साइज़)- छोटा
(प्रतिबिंब की प्रकृति)-वास्तविक एवं उल्टा
(बिंब की स्थिति)- C पर
(प्रतिबिंब की स्थिति)- C पर
(प्रतिबिंब का साइज़)- समान साइज़
(प्रतिबिंब की प्रकृति)-वास्तविक एवं उल्टा
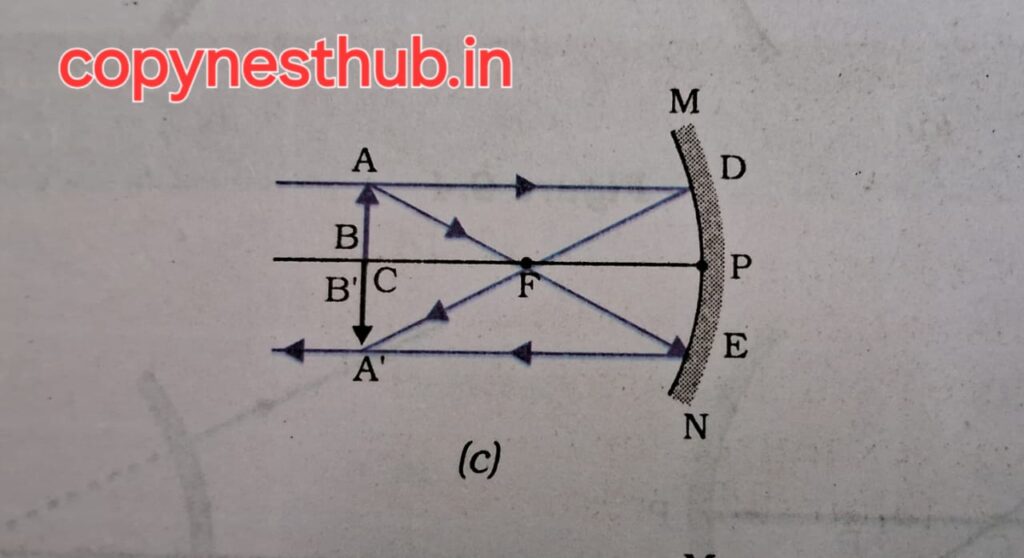
(बिंब की स्थिति)- C और F के बीच
(प्रतिबिंब की स्थिति)- C से परे
(प्रतिबिंब का साइज़)- विवर्धित (बड़ा)
(प्रतिबिंब की प्रकृति)-वास्तविक एवं उल्टा
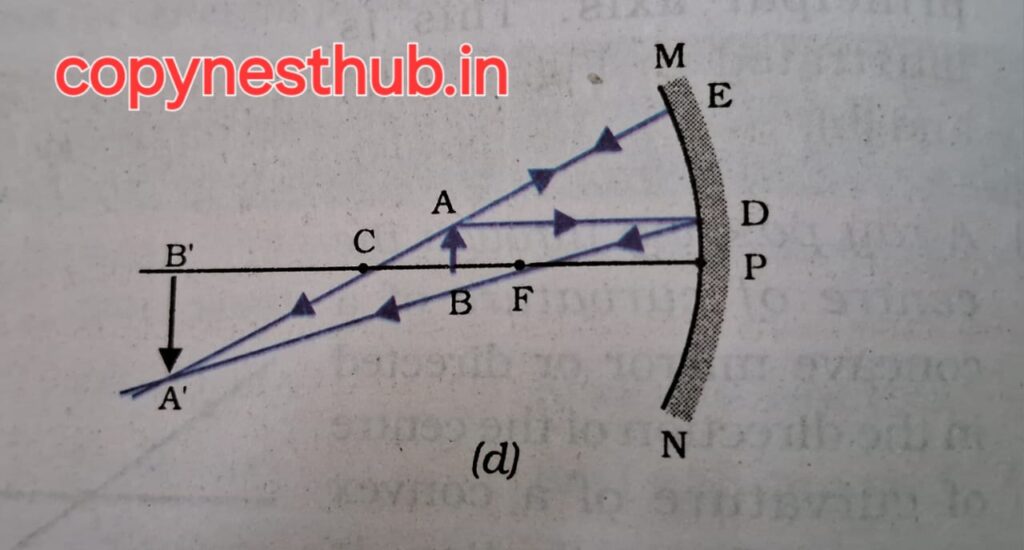
(बिंब की स्थिति)- F पर
(प्रतिबिंब की स्थिति) अनंत पर
(प्रतिबिंब का साइज़)- अत्यधिक विवर्धित
(प्रतिबिंब की प्रकृति)-वास्तविक एवं उल्टा
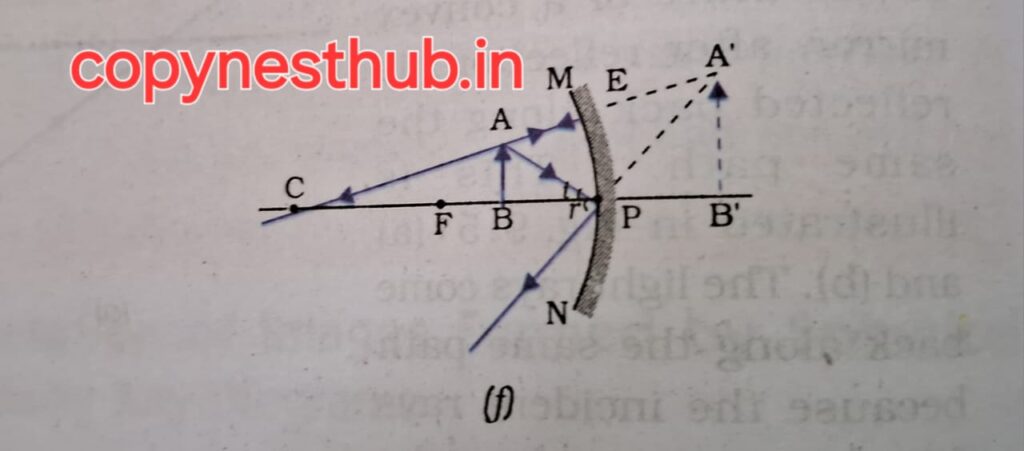
(बिंब की स्थिति)- P और F के बीच
(प्रतिबिंब की स्थिति)- दर्पण के पीछे
(प्रतिबिंब का साइज़)- विवर्धित (बड़ा)
(प्रतिबिंब की प्रकृति) आभासी एवं सीधा
अवतल दर्पण का उपयोग:-
1-टॉर्च
2-सर्च लाइट
3-वाहनों का अग्रदीप
4-शेविंग दर्पण
5-सौर भट्ठी इत्यादि।
किसी उत्तल दर्पण द्वारा बिंब की विभिन्न स्थितियों के लिए बने प्रतिबिंब: –
(बिंब की स्थिति)- अनंत पर
(प्रतिबिंब की स्थिति)- फोकस F पर दर्पण के पीछे
(प्रतिबिंब का साइज़)- अत्यधिक छोटा,बिंदु साइज
(प्रतिबिंब की प्रकृति)- आभासी तथा सीधा
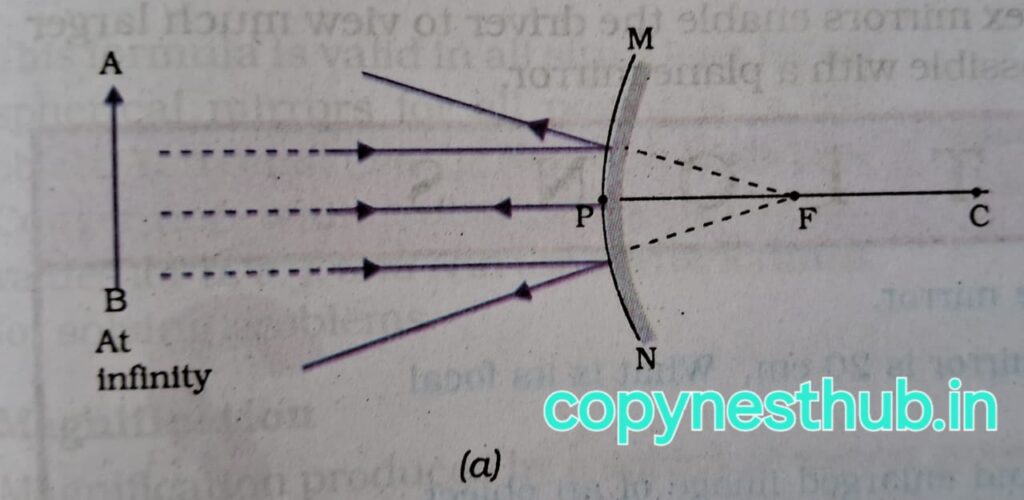
(बिंब की स्थिति)- अनंत तथा दर्पण के ध्रुव P के बीच
(प्रतिबिंब की स्थिति)- P तथा F के बीच दर्पण के पीछे
(प्रतिबिंब का साइज़)- छोटा
(प्रतिबिंब की प्रकृति)- आभासी एवं सीधा
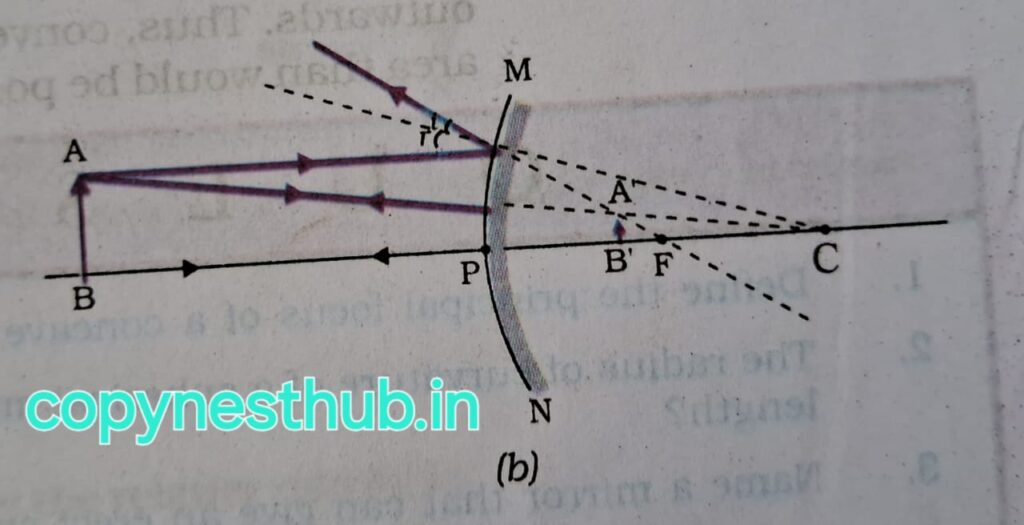
उत्तल दर्पण का उपयोग वाहनों के पश्च-दृश्य दर्पण के रूप में किया जाता है।
समतल दर्पण के इतर उत्तल दर्पण को इसलिए भी प्राथमिकता दिया जाता है क्योंकि यह सदैव सीधा प्रतिबिंब बनाते हैं, यद्यपि वह छोटा होता है।इनका दृष्टि क्षेत्र भी बहुत अधिक है क्योंकि यह बाहर की ओर वक्रित होते हैं अतः समतल दर्पण की तुलना में उत्तल दर्पण वाहन ड्राइवर को अपने पीछे के बहुत बड़े क्षेत्र को देखने में समर्थ बनाते हैं।
गोलीय दर्पणों द्वारा परावर्तन के लिए चिन्ह परिपाटी:-
गोलीय दर्पण द्वारा प्रकाश के परावर्तन पर विचार करते समय हम एक निश्चित चिन्ह परिपाटी का पालन करेंगे, जिसे नयी चिन्ह परिपाटी कहते हैं। इस परिपाटी में दर्पण के ध्रुव (P) को मूल बिंदु मानते हैं। दर्पण के मुख्य अक्ष को निर्देशांक पद्धति का x-अक्ष लिया जाता है।यह परिपाटी निम्न प्रकार है: –
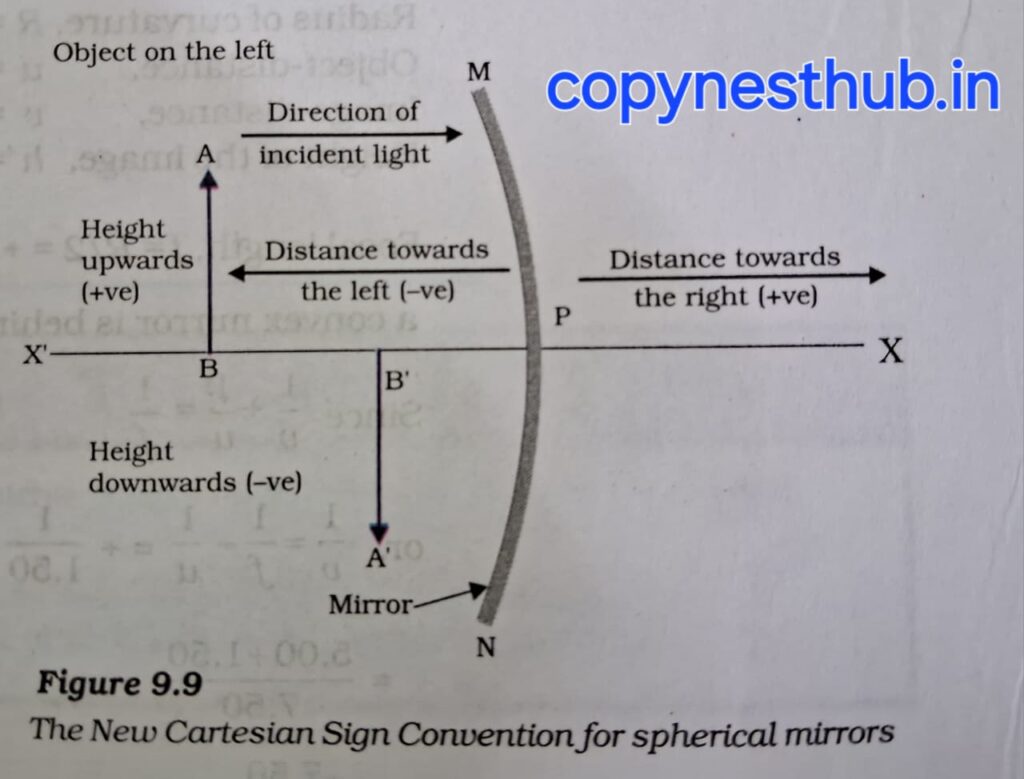
1-बिंब सदैव दर्पण के बायी ओर रखा जाता है। इसका अर्थ है कि दर्पण पर बिंब से प्रकाश बाई ओर से प्राप्त होगा।
2-मुख्य अक्ष के समांतर सभी दूरियां दर्पण के ध्रुव से मापी जाती हैं।
3-मूल बिंदु से दाएं ओर माफी के सभी दूरियां धनात्मक मानी जाती हैं,जबकि मूल बिंदु से बाई और मापी गई दूरियां ऋणात्मक मानी जाती हैं।
4-मुख्य अक्ष के लंबवत तथा ऊपर की ओर मापी जाने वाली दूरियां धनात्मक मानी जाती हैं।
5-मुख्य अक्ष के लंबवत तथा नीचे की ओर मापी जाने वाली दूरियां ऋणात्मक मानी जाती हैं।
यह चिन्ह परिपाटी दर्पण का सूत्र प्राप्त करने तथा संबंधित आंकिक प्रश्न को हल करने के लिए का मददगार है।
दर्पण सूत्र तथा आवर्धन:-
गोलीय दर्पण में इसके ध्रुव से बिंब की दूरी बिंब दूरी(u) कहलाती है।
दर्पण के ध्रुव से प्रतिबिंब की दूरी प्रतिबिंब दूरी(v) कहलाती है।
ध्रुव से फोकस की दूरी फोकस दूरी(f) कहलाती है।
इन तीन राशियों के बीच एक संबंध है,जिसे दर्पण सूत्र द्वारा प्रस्तुत किया जाता है।
सूत्र:- 1/v+1/u=1/f
यह संबंध सभी प्रकार के गोलीय दर्पण के लिए तथा बिंब की सभी स्थितियों के लिए मान्य है।
आवर्धन:-
गोलीय दर्पण द्वारा उत्पन्न वह विस्तार जिससे ज्ञात होता है कि कोई प्रतिबिंब बिंब की अपेक्षा कितना गुना आवर्धित है।
इसे प्रतिबिंब की ऊंचाई तथा बिंब की ऊंचाई के अनुपात के रूप में व्यक्त किया जाता है।
सूत्र: आवर्धन(m)=h’/h
h’= प्रतिबिंब की ऊंचाई
h= बिंब की ऊंचाई
आवर्धन(m) बिंब दूरी(u) तथा प्रतिबिंब दूरी(v) से भी संबंधित है। इसे व्यक्त किया जाता है:-
सूत्र:- m= h’/h= -v/u
आभासी प्रतिबिंबों के लिए बिंब की ऊंचाई धनात्मक लेनी चाहिए। वास्तविक प्रतिबिंबों के लिए बिंब की ऊंचाई ऋणात्मक लेनी चाहिए।
आवर्धन में ऋणात्मक चिन्ह से ज्ञात होता है कि प्रतिबिंब वास्तविक है।आवर्धन में धनात्मक चिन्ह बताता है कि प्रतिबिंब आभासी है।
|| 1.3 || TOPIC NO.3- प्रकाश का अपवर्तन ||
अपवर्तन- जब प्रकाश की किरणें एक माध्यम से दूसरे माध्यम में जाती हैं,तो वे अपने मार्ग से विचलित हो जाती हैं,इस घटना को प्रकाश का अपवर्तन (Refraction) कहते हैं।

अपवर्तन प्रकाश की पारदर्शी माध्यम से दूसरे में प्रवेश करने पर प्रकाश की चाल में परिवर्तन के कारण होता है।
प्रकाश का अपवर्तन निश्चित नियमों के आधार पर होता है। परावर्तन के नियम निम्नलिखित हैं: –
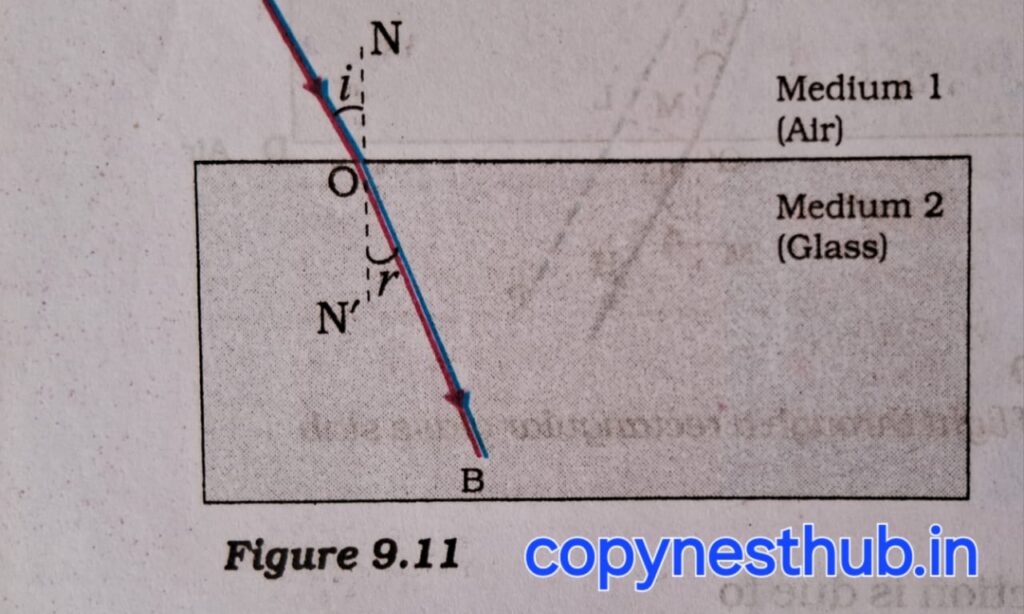
1-आपतित किरण,अपर्तित किरण तथा दोनों माध्यमों को पृथक करने वाले पृष्ठ के आपतन बिंदु पर अभिलंब सभी एक ही तल में स्थित होते हैं।
2-प्रकाश के किसी निश्चित रंग तथा निश्चित माध्यमों के युग्म के लिए आपतन कोण की ज्या (Sine) तथा अपवर्तन कोण की ज्या (Sine) का अनुपात स्थिर होता है।इस नियम को “स्नेल का अपवर्तन का नियम” भी कहा जाता है। यदि i आपतन कोण तथा r अपवर्तन कोण हो तब:-
Sin i/sin r=स्थिरांक
इस स्थिरांक के मान को दूसरे माध्यम का पहले माध्यम के सापेक्ष अपवर्तनांक (Refractive Index) कहते हैं।
अपवर्तनांक:-
प्रकाश की किरण तिरछी गमन करती हुई एक पारदर्शी माध्यम से दूसरे में प्रवेश करती है तो यह दूसरे माध्यम में अपनी दिशा परिवर्तित कर लेती है। किन्ही दिए हुए माध्यमों के युग्म के लिए होने वाले दिशा परिवर्तन की विस्तार को अपवर्तनांक के रूप में व्यक्त किया जाता है। यह एक स्थिरांक है।
विभिन्न माध्यमों में प्रकाश अलग-अलग चालों से संचारित होता है।निर्वात में प्रकाश की अधिकतम चाल 3,00,000km/s होती हैं।(प्रकाश की सबसे तेज चाल)
दो माध्यमों के युग्म के लिए अपवर्तनांक का मान दोनों माध्यमों में प्रकाश की चाल पर निर्भर करता है।
अगर हम एक प्रकाश की किरण पर विचार करें जो माध्यम 1 से माध्यम 2 में प्रवेश कर रही है: –
मान लीजिए प्रकाश की चाल माध्यम 1 में v1 तथा मध्यम 2 में v2 है। माध्यम 2 का माध्यम 1 के सापेक्ष अपवर्तनांक माध्यम 1 में प्रकाश की चाल तथा माध्यम 2 में प्रकाश की चाल के अनुपात द्वारा व्यक्त करते हैं। इसे प्राय: संकेत n21 से निरूपित किया जाता है। इसे समीकरण के रूप में निम्न प्रकार से व्यक्त कर सकते हैं:-
n21=माध्यम 1 में प्रकाश की चाल /माध्यम 2 में प्रकाश की चाल
n12=माध्यम 2 में प्रकाश की चाल /माध्यम 1 में प्रकाश की चाल
माध्यम 1 एक निर्वात या वायु है तब माध्यम 2 का अपवर्तनांक निर्वात के सापेक्ष माना जाता है।यह माध्यम का निरपेक्ष अपवर्तनांक कहलाता है। यह केवल n2 से निरूपित किया जाता है। यदि वायु में प्रकाश की चाल c है तथा माध्यम में प्रकाश की चाल v है,तब माध्यम का अपवर्तनांक nm होगा।
nm=वायु में प्रकाश की चाल(c)/ माध्यम में प्रकाश की चाल (v)=c/v
माध्यम का निरपेक्ष अपवर्तनांक केवल अपवर्तनांक कहलाता है।
1-वायु का अपवर्तनांक 1.003
2-बर्फ का अपवर्तनांक 1.31
3-जल का अपवर्तनांक 1.33
4-एल्कोहल का अपवर्तनांक 1.36
5-केरोसिन का अपवर्तनांक 1.44
6-हीरा का अपवर्तनांक 2.42
जल का अपवर्तनांक 1.33 का अर्थ है कि वायु में प्रकाश का वेग तथा जल में प्रकाश के वेग का अनुपात 1.33 है।
किसी माध्यम की प्रकाश को अपवर्तित करने की क्षमता को उसके प्रकाशित घनत्व के द्वारा भी व्यक्त किया जा सकता है।
दो माध्यमों की तुलना करते समय अधिक अपवर्तनांक वाला माध्यम दूसरे की अपेक्षा प्रकाशिक संघन है।
दूसरा कम अपवर्तनांक वाला माध्यम प्रकाशित विरल माध्यम है।विरल माध्यम में प्रकाश की चाल सघन माध्यम की अपेक्षा अधिक होती है,अतः विरल माध्यम से सघन माध्यम में गमन करने वाली प्रकाश की किरणें धीमी हो जाती हैं तथा अभिलंब की ओर झुक जाती हैं। जब यह सघन माध्यम से विरल माध्यम में गमन करती है तो उसकी चाल बढ़ जाती है तथा यह अभिलंब से दूर हट जाती हैं।
गोलीय लेंस द्वारा अपवर्तन:-
दो पृष्ठों से घिरा हुआ कोई पारदर्शी माध्यम जिनका एक या दोनों पृष्ठ गोलीय है, लेंस कहलाता है।
किसी लेंस में बाहर की ओर उभरे दो गोलीय पृष्ठ हो सकते हैं। ऐसे लेंस को द्वि- उत्तल लेंस कहते हैं।इसे केवल उत्तल लेंस भी कहते हैं।यह किनारो की अपेक्षा बीच में मोटा होता है।इसे अभिसारी लेंस भी कहते हैं।
द्वि-अवतल लेंस अंदर की ओर वक्रित दो गोलीय पृष्ठों से घिरा होता है। इसे अवतल लेंस भी कहा जाता है।यह बीच की अपेक्षा किनारो से मोटा होता है।इसे अपसारी लेंस भी कहते हैं।
किसी लेंस में चाहे वह उत्तल हो या अवतल दो गोलीय पृष्ठ होते हैं।इनमें से प्रत्येक पृष्ठ एक गोले का भाग होता है। इन गोलों का केंद्र लेंस के वक्रता केंद्र कहलाते हैं।
लेंस का वक्रता केंद्र प्रायः अक्षर C द्वारा निरूपित किया जाता है, क्योंकि लेंस के दो वक्रता केंद्र है इसलिए इन्हें C1 तथा C2 द्वारा निरूपित किया जाता है।
किसी लेंस के दोनों वक्रता केंद्रों से गुजरने वाली एक काल्पनिक सीधी रेखा लेंस की मुख्य अक्ष कहलाती है।
लेंस का केंद्रीय बिंदु उसका प्रकाशिक केंद्र कहलाता है। ।इसे प्रायः अक्षर O से निरूपित किया जाता है।
लेंस के प्रकाशित केंद्र से गुजरने वाली प्रकाश किरण बिना किसी विचलन के निर्गत होती है।
गोलीय लेंस की वृताकार रूपरेखा का प्रभावी व्यास इसका द्वारा कहलाता है।
उत्तल लेंस पर मुख्य अक्ष के समांतर प्रकाश की बहुत सी किरणें आपतित हैं। यह किरण लेंस के अपवर्तन के पश्चात मुख्य अक्ष पर एक बिंदु पर अभिसारित हो जाती हैं। मुख्य अक्ष पर यह बिंदु लेंस का मुख्य फोकस कहलाता है।
अवतल लेंस पर मुख्य अक्ष के समांतर प्रकाश की अनेक किरणें आपतित हो रही हैं। यह किरणें लेंस से अपवर्तन के पश्चात मुख्य अक्ष के एक बिंदु से अपसरित होती प्रतीत होती हैं। मुख्य अक्ष पर यह बिंदु अवतल लेंस का मुख्य फोकस कहलाता है।
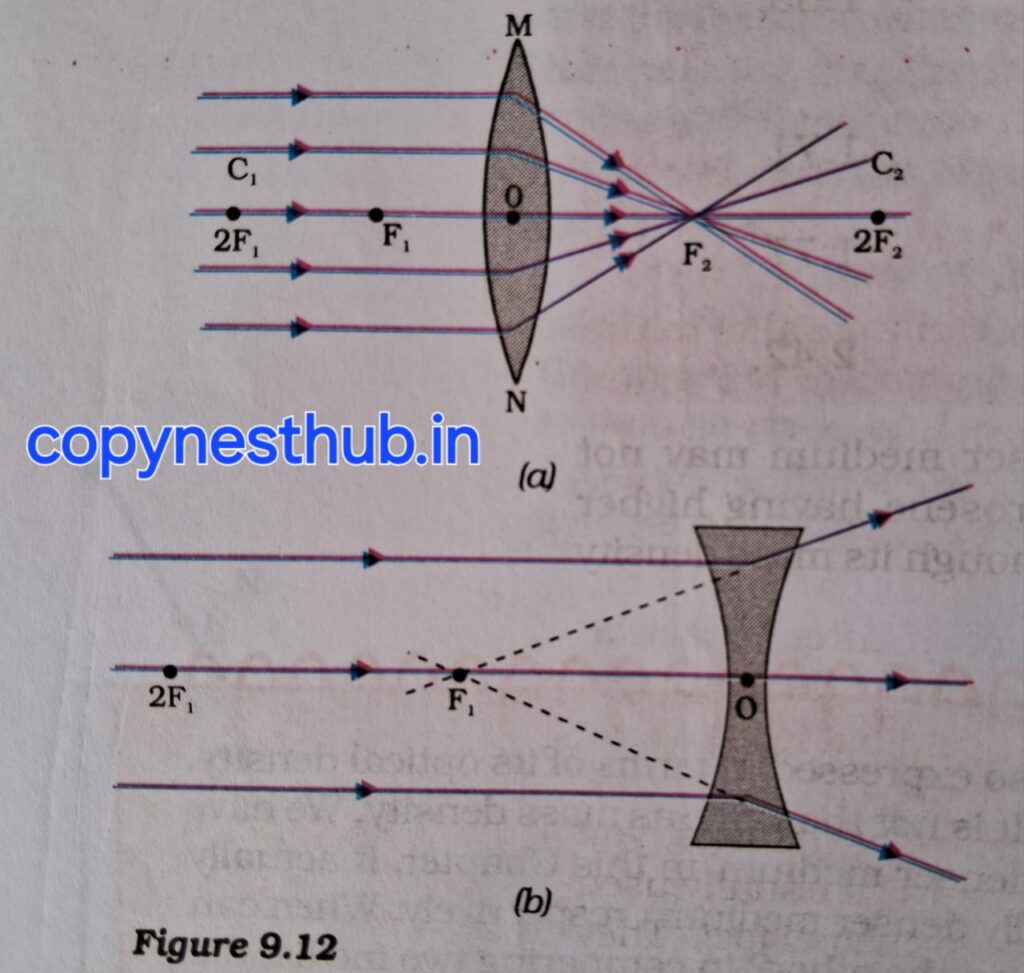
किसी लेंस में दो मुख्य फोकस होते हैं।। इन्हें F1 तथा F2 द्वारा निरूपित किया जाता है।किसी लेंस के मुख्य फोकस की प्रकाशिक केंद्र से दूरी फोकस दूरी कहलाती है।फोकस दूरी को अक्षर f द्वारा निरूपित किया जाता है।
किरण आरेखों के उपयोग द्वारा लेंस से प्रतिबिंब बनना:-
लेंस में किरण आरेख बनाने के लिए हम निम्न में से किन्ही दो किरणों पर विचार कर सकते हैं: –
1-बिंब से मुख्य अक्ष के समांतर आने वाली कोई प्रकाश किरण उत्तल लेंस से अपवर्तन के पश्चात लेंस की दूसरी ओर मुख्य फोकस से गुजरेगी। अवतल लेंस की स्थिति में प्रकाश किरण लेंस के उसी ओर स्थित मुख्य फोकस से अपसरित होती प्रतीत होगी।
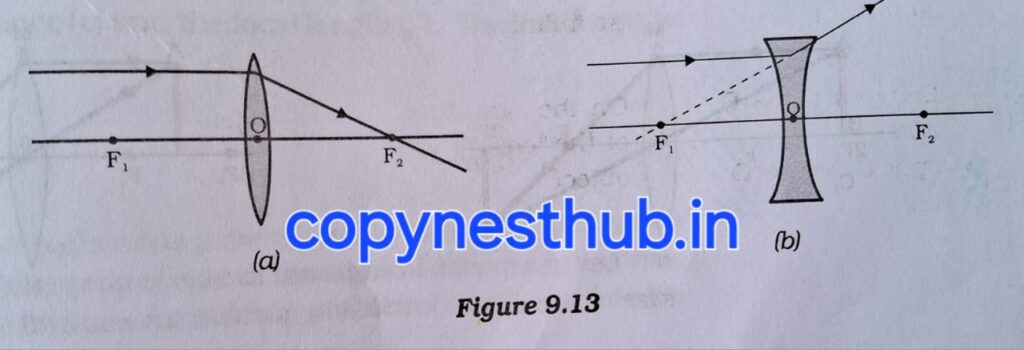
2-मुख्य फोकस से होकर गुजरने वाली प्रकाश किरण उत्तल लेंस से अपवर्तन के पश्चात मुख्य अक्ष के समांतर निर्गत होगी। अवतल लेंस की मुख्य फोकस पर मिलती प्रतीत होने वाली प्रकाश किरण, अपवर्तन के पश्चात मुख्य अक्ष के समांतर निर्गत होगी।
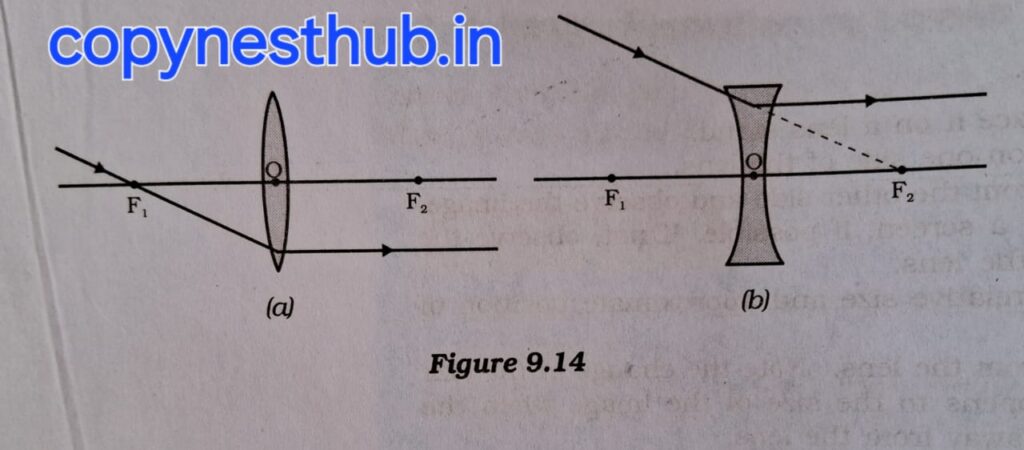
3-लेंस के प्रकाशिक केंद्र से गुजरने वाली प्रकाश किरण अपवर्तन के पश्चात बिना किसी विचलन के निर्गत होगी।
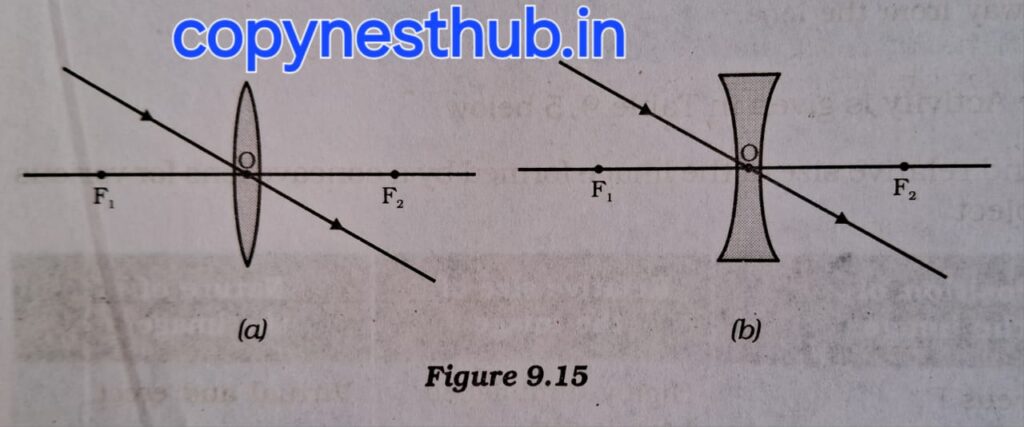
लेंस द्वारा प्रतिबिंब बनना:-
लेंस प्रकाश के अपवर्तन द्वारा प्रतिबिंब बनाते हैं।
उत्तल लेंस द्वारा बने प्रतिबिंब की प्रकृति, स्थिति तथा अपेक्षित साइज : –
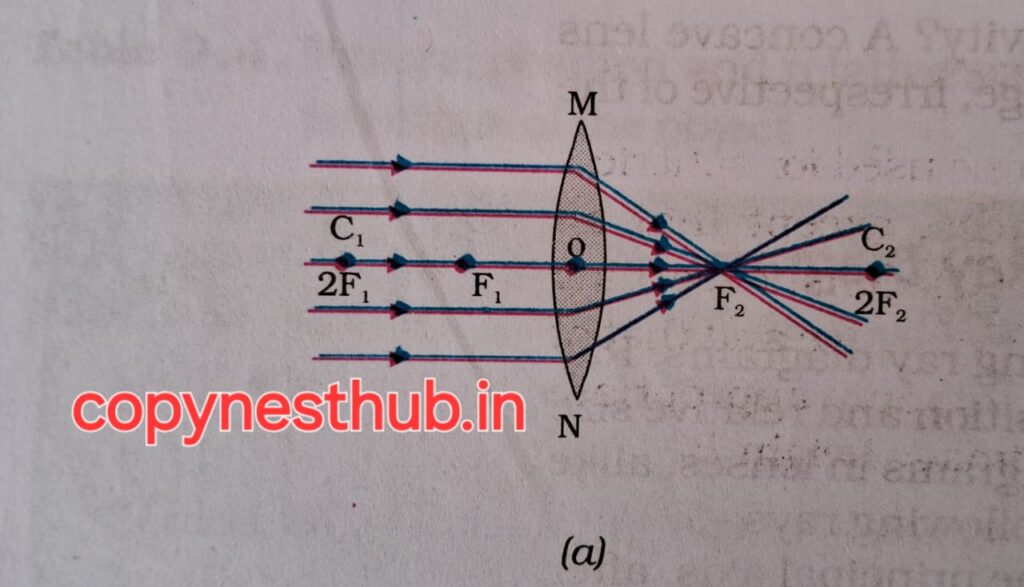
(बिंब की स्थिति)- अनंत पर
(प्रतिबिंब की स्थिति) फोकस F2 पर
(प्रतिबिंब का साइज़)- अत्यधिक छोटा, बिंदु आकार
(प्रतिबिंब की प्रकृति)-वास्तविक एवं उल्टा
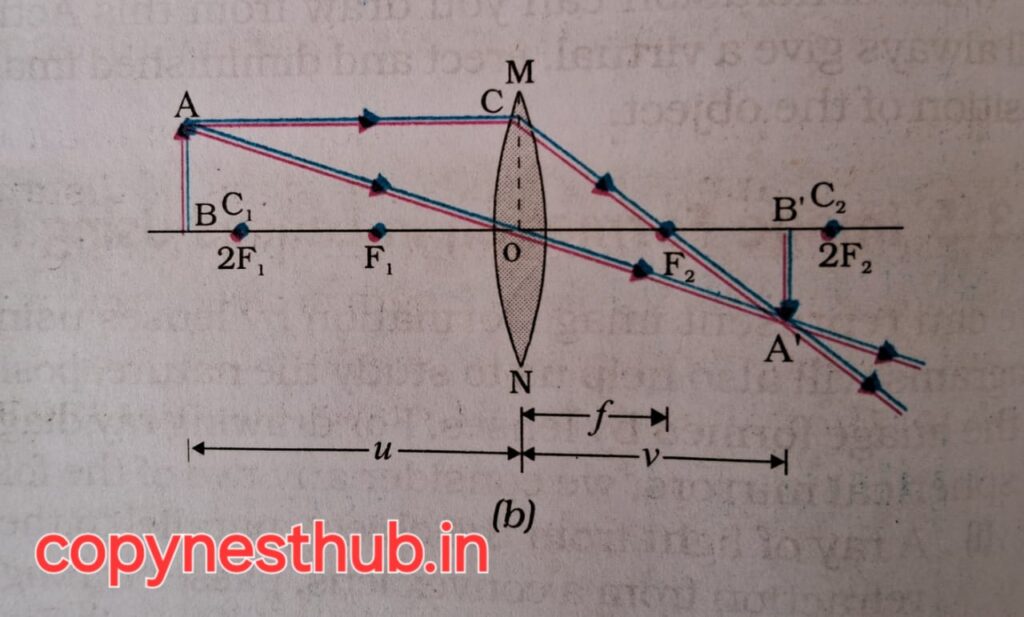
(बिंब की स्थिति)- 2F1 से परे
(प्रतिबिंब की स्थिति)- F2 और 2F2 के बीच
(प्रतिबिंब का साइज़)- छोटा
(प्रतिबिंब की प्रकृति)-वास्तविक एवं उल्टा
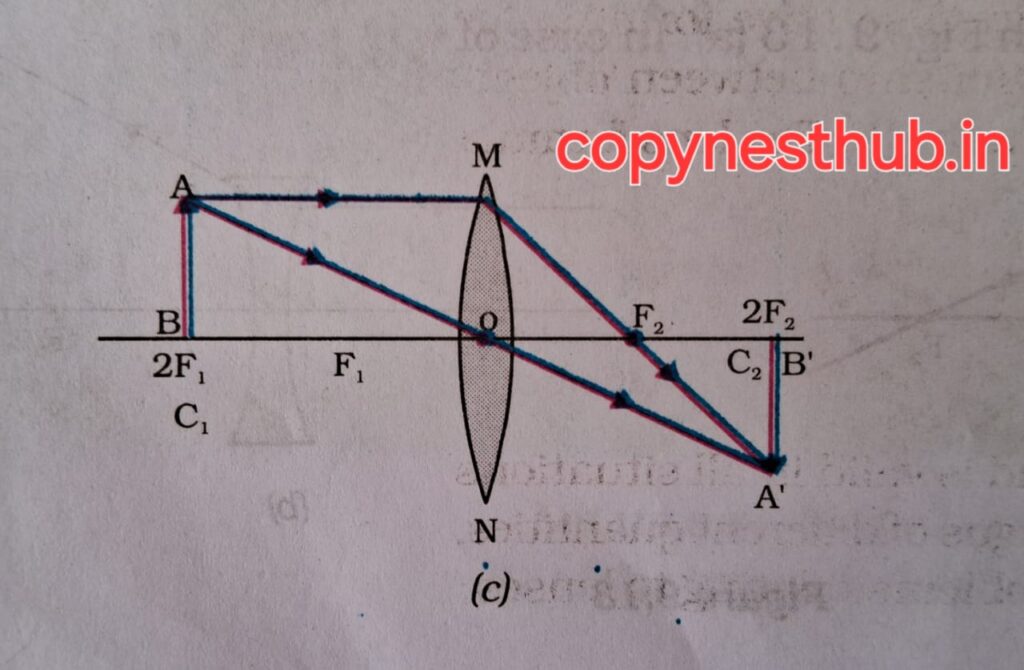
बिंब की स्थिति)-2F1 पर
(प्रतिबिंब की स्थिति)- 2F2 पर
(प्रतिबिंब का साइज़)- समान साइज़
(प्रतिबिंब की प्रकृति)-वास्तविक एवं उल्टा
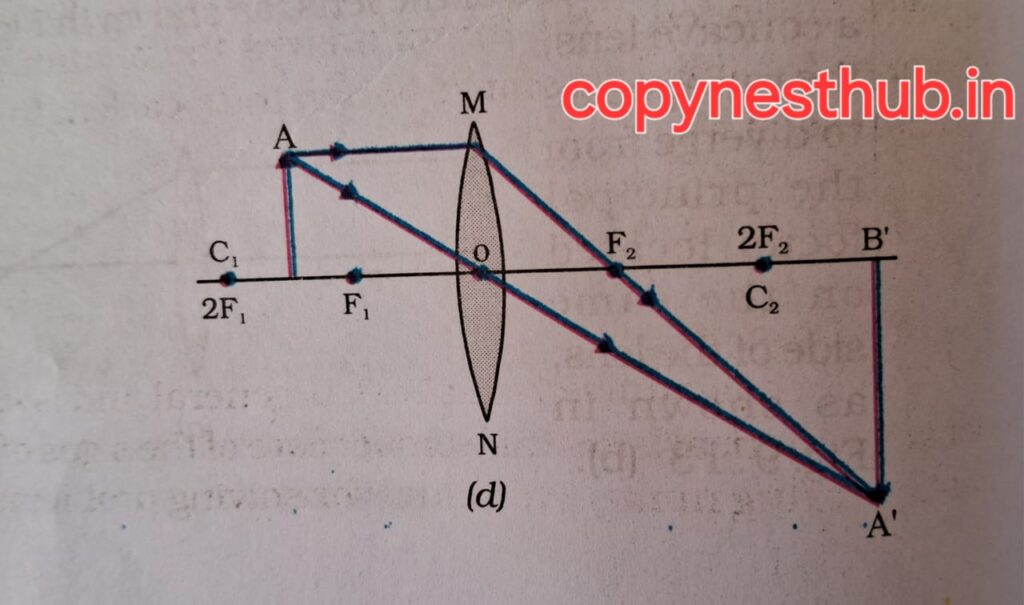
बिंब की स्थिति)- F1 तथा 2F1 के बीच
(प्रतिबिंब की स्थिति)- 2F2 से परे
(प्रतिबिंब का साइज़)- बड़ा (विवर्धित)
(प्रतिबिंब की प्रकृति)-वास्तविक एवं उल्टा
बिंब की स्थिति) फोकस F1 पर
(प्रतिबिंब की स्थिति)- अनंत पर
(प्रतिबिंब का साइज़)- अत्यधिक विवर्धित
(प्रतिबिंब की प्रकृति)-वास्तविक एवं उल्टा
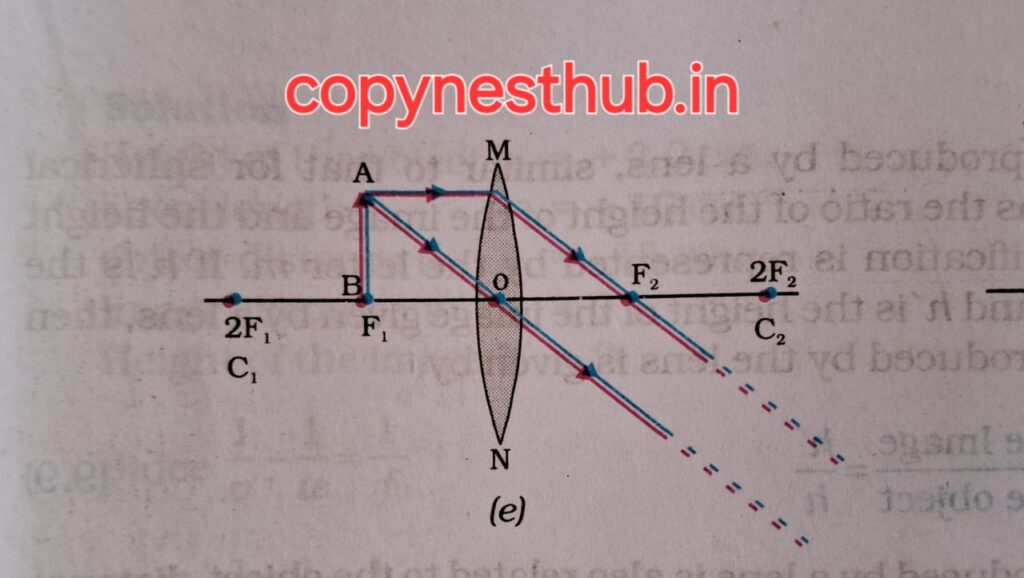
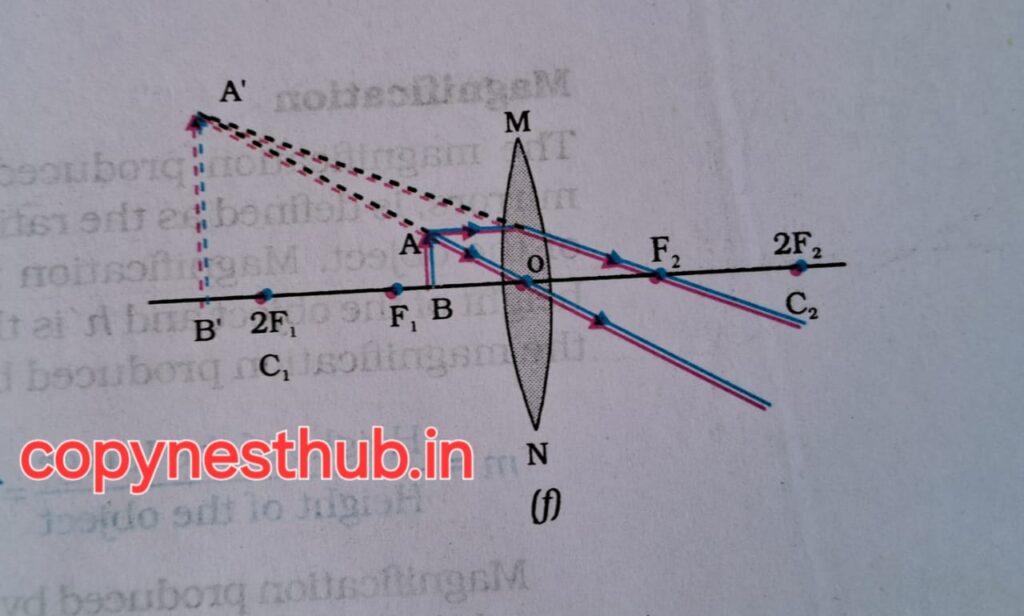
बिंब की स्थिति)- फोकस F1 तथा प्रकाशिक केंद्र O के बीच
(प्रतिबिंब की स्थिति)- जिस ओर बिंब है,लेंस के उसी ओर
(प्रतिबिंब का साइज़)- बड़ा (विवर्धित)
(प्रतिबिंब की प्रकृति)-आभासी तथा सीधा
अवतल लेंस द्वारा बने प्रतिबिंब की प्रकृति, स्थिति तथा अपेक्षित साइज : –
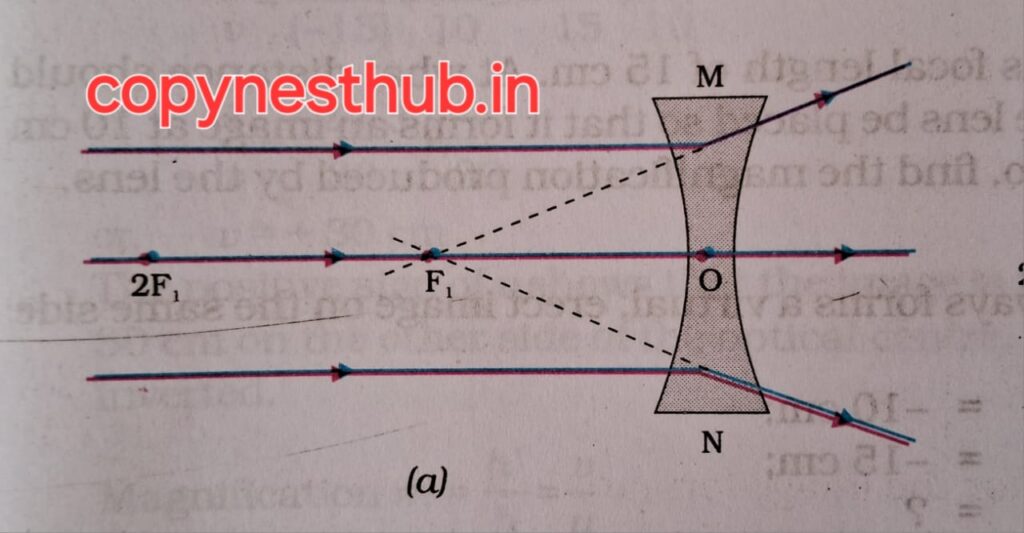
बिंब की स्थिति)- अनंत पर
(प्रतिबिंब की स्थिति)- फोकस F1 पर
(प्रतिबिंब का साइज़)- अत्यधिक छोटा, बिंदु आकर
(प्रतिबिंब की प्रकृति)-आभासी तथा सीधा
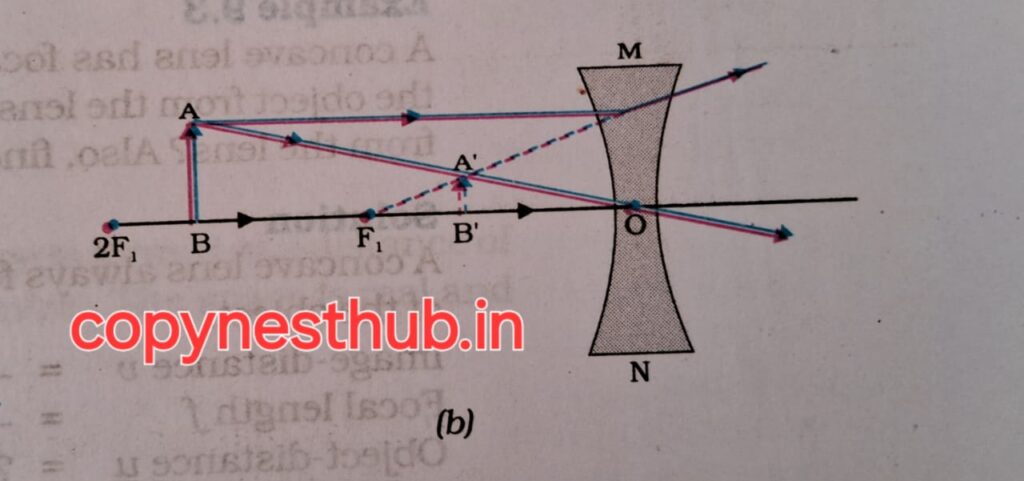
बिंब की स्थिति) अनंत तथा लेंस के प्रकाशिक केंद्र O के बीच
(प्रतिबिंब की स्थिति) फोकस F1 तथा प्रकाशिक केंद्र O के बीच
(प्रतिबिंब का साइज़) छोटा
(प्रतिबिंब की प्रकृति)-आभासी तथा सीधा
गोलीय लेंस के लिए चिन्ह परिपाटी:-
जहां दर्पणों में सभी दूरियां उनके ध्रुव से नापी जाती थी वहां लेंस में सभी दूरियां उनके प्रकाशित केंद्र से लिए जाते हैं।
परिपाटी के अनुसार उत्तल लेंस की फोकस दूरी धनात्मक होती है, जबकि अवतल लेंस की फोकस दूरी ऋणात्मक होती है।
लेंस सूत्र तथा आवर्धन: –
बिंब दूरी(u) प्रतिबिंब दूरी और फोकस दूरी के बीच इन तीन राशियों के बीच एक संबंध है,जिसे लेंस सूत्र द्वारा प्रस्तुत किया जाता है।
सूत्र:- 1/v- 1/u=1/f
यह लेंस सूत्र किसी भी गोलीय लेंस के लिए सभी स्थितियों में मान्य है।
आवर्धन:-
यदि बिंब की ऊंचाई h हो तथा लेंस द्वारा बनाए गए प्रतिबिंब की ऊंचाई h’ हो,तब लेंस द्वारा उत्पन्न आवर्धन होगा-
सूत्र:- आवर्धन (m)=h’/h
आवर्धन(m) बिंब दूरी(u) तथा प्रतिबिंब दूरी(v) से भी संबंधित है। इसे व्यक्त किया जाता है:-
सूत्र:- m= h’/h= v/u
लेंस की क्षमता:-
किसी लेंस की प्रकाश किरणों को अभिसरित तथा अपसरित करने की क्षमता इसकी फोकस दूरी पर निर्भर करती है।
उदाहरण – कम फोकस दूरी का एक उत्तल लेंस प्रकाश किरणों को बड़े कोण से मोड़कर उन्हें प्रकाशित केंद्र के निकट फोकसित कर देता है।
किसी लेंस द्वारा प्रकाश किरणों को अभिसरण या अपसरण करने की मात्रा को उसकी क्षमता के रूप में व्यक्त किया जाता है। इसे अक्षर P द्वारा निरूपित किया जाता है।
किसी f फोकस दूरी के लेंस की क्षमता होती है:-
सूत्र:- P=1/f
f मीटर में होता है।
लेंस की क्षमता का S.I मात्रक डाइऑप्टर(Dioptre)होता है। इसे अक्षर D द्वारा दर्शाया जाता है।
1 डाइऑप्टर (Dioptre) उस लेंस की क्षमता है जिसकी फोकस दूरी 1 मीटर हो।
उत्तल लेंस की क्षमता धनात्मक तथा अवतल लेंस की ऋणात्मक होती है।
THANKS FOR READING…